1) 90°<143°<180° - Вторая четверть, sin143°>0 , cos143°<0 , tg143°<0 , ctg143°<0
2) -243° - вторая четверть. sin(-243°)>0 , cos(-243)°<0 , tg(-243°)<0 , ctg(-243°)<0
3) 735° . Весь круг - 360° , 360 * 2 =720° + ещё немного. Это значит, что 735° в 1 четверти. sin735°>0, cos735°>0 , tg735° и ctg 735° > 0.
4)-735°. -735° в 4 четверти. sin(-735°)<0 , cos(-735°)>0 + , tg(-735°) и ctg(-735°) < 0.
5) 300° - 3 четверть , sin(300°)<0 , cos(300°)<0 + , tg(300°) и ctg(300°) > 0 .
6) 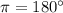 ,
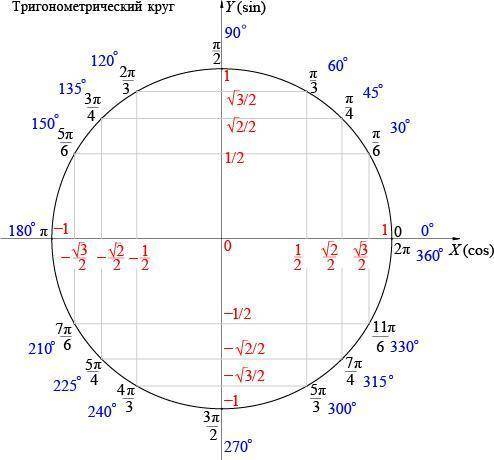
, 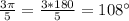 ∈ 2 четверти,
∈ 2 четверти, 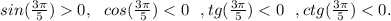
7) 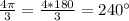 , ∈ 3 четверти ,
, ∈ 3 четверти , 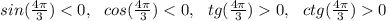
8) 1 радиан ≈ 57° . -0,5 радиан - 4 четверть. sin(-0,5)<0 , cos(-0,5)>0 , tg(-0,5) < 0 ,ctg (-0,5) <0
9) 4 радиана ∈ 3 четверти (4*57°≈228° ), sin4<0 , cos4<0 , tg4>0 , ctg4>0
10) -7,3 ∈ 4 четверти (-7,3*57°≈-416,1°), sin(-7,3) <0 , cos(-7,3) >0 , tg(-7,3) <0 , ctg(-7,3) <0.
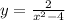
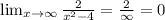
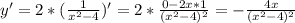
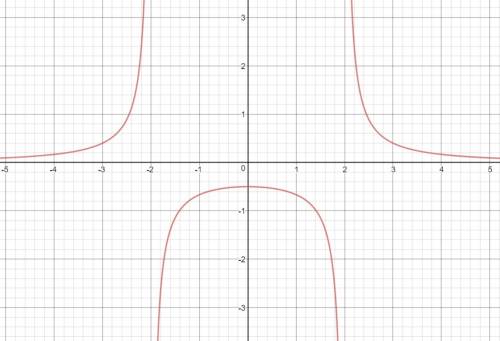
х² - 7х + 12 = х² - 3х - 4х + 12 = х(х - 3) - 4(х - 3) = (х - 3)(х - 4)
с нахождением корней):
★ Сначала найдём корни данного многочлена:
х² - 7х + 12 = 0
По теореме обратной теореме Виета:
х1 + х2 = -(-7) = 7; х1 * х2 = 12 => х1 = 3; х2 = 4
D = (-7)² - 4 * 1 * 12 = 49 - 48 = 1
x1 = (-(-7) + √1)/(2 * 1) = (7 + 1)/2 = 8/2 = 4
x2 = (-(-7) - √1)/(2 * 1) = (7 - 1)/2 = 6/2 = 3
★ Если многочлен 2-ой степени имеет корни, то его разложение на множители имеет следующий вид:
ах² + bx + c = a(x - x1)(x - x2)
Значит, х² - 7х + 12 = 1 * (х - 3)(х - 4) = (х - 3)(х - 4)