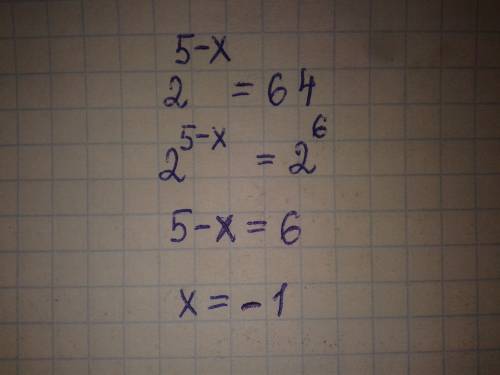
ответ: x=-4, x=0.
Объяснение:
Функция определена и непрерывна на всей числовой оси.
Находим производную и приравниваем её к нулю: y'=3*x²+12*x=3*x*(x+4)=0. Решая это уравнение, находим две критические точки x=0 и x=-4. Если x<-4, то y'>0, поэтому на интервале (-∞; -4) функция возрастает. Если -4<x<0, то y'<0, поэтому на интервале (-4; 0) функция убывает. Если x>0, то y'>0, так что на интервале (0; ∞) функция возрастает. Отсюда следует, что точка x=-4 является точкой максимума, а точка x=0 - точкой минимума функции. Однако эти экстремумы - локальные; наибольшего и наименьшего значения на всей области определения функция не имеет.
рассмотрим наше уравнение:
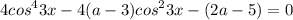
выполним замену cos²3x=t; t≥0
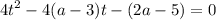
чтобы уравнение имело хотя бы один корень надо чтобы D≥0
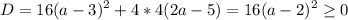
Это неравенство выполняется для любых a
тогда проверим корни, необходимо чтобы t≥0
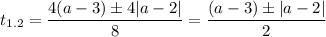
рассмотрим первый корень
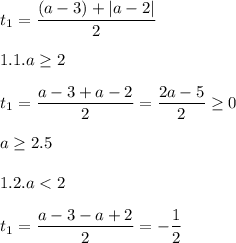
значит при а≥2.5 мы получим один положительный корень (относительно t)
проверим второй корень
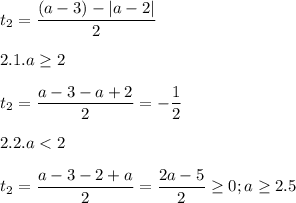
тут положительных корней не получим.
значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5
выполним обратную замену
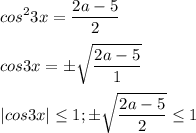
рассмотрим положительный корень
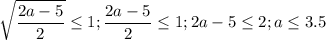
рассмотрим отрицательный корень
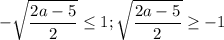
выполняется для всех а≥2.5
Собираем все вместе 2,5≤а≤3,5