ответ: 10^6
Объяснение:
Пусть первая цифра слева семизначного числа отлична от 0 и равна a и существует еще хотя бы одна цифра отличная от 0 ( как минимум она равна 1), тогда независимо от значений остальных цифр числитель всегда будет менее чем (a+1)*10^6, а знаменатель всегда не менее чем (a+1), ибо хотя бы еще одна цифра ненулевая, таким образом, выполняется такое неравенство:
S/S(k) < (a+1)*10^6/(a+1) = 10^6.
Поскольку a>0, то a+1 >0, а значит деления на 0 не возникает.
Рассмотрим оставшийся вариант: все цифры помимо первой равны 0, а первая цифра равна a и также отлична от нуля, тогда:
S/S(k) = a*10^6/a = 10^6
Поскольку a>0, деления на 0 не возникает.
Таким образом, наибольшее значение:
S/S(k) = 10^6.
max {k / S(k)} = 1 000 000
Объяснение:
Цифра в старшем разряде не может быть равна 0, потому что в противном случае число не будет семизначным. Сначала рассмотрим случай, когда это единственная ненулевая цифра в числе k:
Теперь предположим, что в числе есть другие ненулевые цифры и покажем, что в этом случае значение дроби меньше 10⁶. Цифры числа k обозначим через a₆, a₅, ..., a₀.
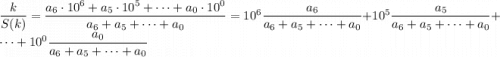
Рассмотрим дробь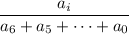 
, где 
– одна из цифр числа k. Заметим, что 
для любых x>0 и y≥0. Тогда если мы оставим в знаменателе этой дроби только два слагаемых, одно из которых (ai) присутствует в числителе, а второе (aj) не равно нулю, будет верно неравенство:
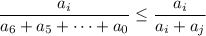
Если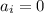 
, то 
. В противном случае мы можем поделить числитель и знаменатель дроби на : 
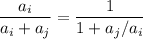, а поскольку ai и aj – это некоторые отличные от нуля цифры, максимально возможное значение этой дроби достигается при ai=9 и aj=1: 
.
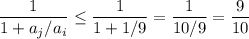Из этого следует, что 
.
Теперь вернемся к исходному отношению k/S(k) при наличии хотя бы двух отличных от нуля цифр:
Таким образом, мы доказали, что максимальное значение дроби k/S(k) равно 10⁶ = 1000000 и достигается, когда все все цифры числа k, кроме первой, равны нулю.
5x^2+20x+20+6x-44=0
5x^2+26x-24=0
D=676-4*5*(-24)=1156
X1=-26-√1156/10=-26-34/10=-6
X2=-26+√1156/10=-26+34/10=8/10=0.8