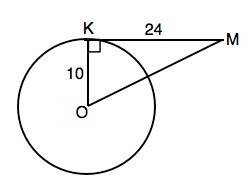
Обозначим центр окружности О, точку касания К.
Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∆ МОК - прямоугольный.
Отношение катетов 10:24=5:12 указывает на то, что длины сторон треугольника из Пифагоровых троек 5:12:13, в которых эти длины –целые числа.⇒ МО=2•13=26. И это можно проверить по т.Пифагора.
МО=√(KO²+KM²)=√676=26
В прямоугольном треугольнике каждый катет является высотой, проведенной к другому катету.
Площадь прямоугольного треугольника равна половине произведения катетов:
S=КМ•КО:2=24•10:2=120 см²
Из них благоприятные исходы можно перечислить:
1+6
6+1
2+5
5+2
3+4
4+3
Таким образом, всего благоприятных исходов 6.
Вероятность найдем, как отношение числа 6 благоприятных исходов к числу всех возможных комбинаций 36.
6/36 = 0,16666…
Округлим до сотых. ответ: 0, 17