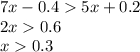
В решении.
Объяснение:
Какова область определения функции у = 5/√8х - 4х²?
Область определения - это значения х, при которых функция существует, проекция графика на ось Ох.
Обозначение D(f) или D(у).
Дана функция у = 5/√8х - 4х²
Так как в данном выражении в знаменателе корень, подкоренное выражение должно быть больше либо равно нулю.
Функция определена, если знаменатель не равен нулю.
Поэтому найти значения х через неравенство:
8х - 4х² > 0
Приравнять к нулю и решить как квадратное уравнение:
8х - 4х² = 0 (неполное квадратное уравнение)
4х(2 - х) = 0
Приравнять множители поочерёдно к нулю:
4х = 0
х₁ = 0;
2 - х = 0
-х = -2
х₂ = 2.
При х=0 и х=2 подкоренное выражение равно нулю, что не допустимо.
Поэтому х может быть любым, кроме х=0 и х=2.
Область определения D(у) = х∈R : х≠0; х≠2.
Для отыскания наибольшего(наименьшего) значения функции существует один и тот же приём:
1) ищем производную.
2) приравниваем её к нулю и ищем корни.
3) смотрим , какие корни входят в указанный промежуток.
4)ищем значения данной функции на концах указанного промежутка и в точках, входящих в указанный промежуток.
5) пишем ответ.
Начали.
y = x³ -3x² +7x -5 [1;4]
y' = 3x² -6x +7
3x² -6x +7 = 0
D<0 корней нет
х = 1
у = 3*1² -6*1 +7 *1 -5 = -1
х = 4
у = 3*4³ -3*4²+7*4 -5 = 192 - 48 +28 -5 = 163
ответ: max y = 163
min y = -1