Поиск...
Избавься от ограничений
TOP_BANNER_BUTTON_NO_TRIAL
bellfam12
bellfam12
16.08.2018
Алгебра
5 - 9 классы
ответ дан
Найти координаты точки пересечения графиков функций:
1) y=-2x+7 и y=0,5x-5,5
2) y=4x и y=-x+10
3) y=1-2x и y=x-5
2
ПОСМОТРЕТЬ ОТВЕТЫ
Войди чтобы добавить комментарий
ответ
5,0/5
5
Guardian07
светило науки
693 ответов
300 тыс. пользователей, получивших
Решение во вложении. Удачи!
dome7w и 8 других пользователей посчитали ответ полезным!
5
5,0
(3 оценки)
Войди чтобы добавить комментарий
ответ
4,5/5
2
армения20171
главный мозг
3.5 тыс. ответов
4.7 млн пользователей, получивших
1)у=-2х+7 и у=0,5х-5,5
ординаты точки пересечения равни
y-2х+7=0,5х-5,5
-2,5х=-12,5
х=12,5:2,5
х=5
у=-2х+7=-10+7=-3
точка пересечения А(5;-3)
2)у=4х и у=-х+10
4х=-х+10
5х=10
х=2
у=4х=8
В(2;8)
3)у=1-2х и у=х-5
1-2х=х-5
-3х=-6
х=2
у=х-5=2-5=-3
С(2;-3)
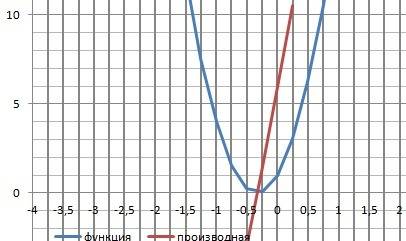
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет
2. Пересечение с осью Х. Решаем квадратное уравнение: Y=0
при х1,2 = - 1/3.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞ - горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = 9*x² - 6*x+1 ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 18*x -6 = 0.
Корень Х= -1/3.
7. Локальные экстремумы. Минимум – Ymin(- 1/3) =0.
8. Интервалы возрастания и убывания. Возрастает - Х∈(-1/3;+∞),
убывает = Х∈(-∞;-1/3)
8. Вторая производная - Y"(x) = 18.
Корня производной - точка перегиба - нет.
9. Вогнутая – «ложка» Х∈(-∞;+∞).
10. Область значений Е(у) У∈(0;+∞)
11. Наклонная асимптота -. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(∞)(9x+6+1)= ∞ - наклонных асимптот - нет
12. График в приложении.
x^5-3x^3+4x^2-12=x^3(x^2-3)+4(x^2-3)=(x^3+4)(x^2-3)
2)20a^3bc-28ac^2+15a^2b^2-21bc=
(объединим 1 и 3 слагаемое, а также 2 и 4)
=5a^2b(4ac+3b) - 7c(4ac+3b)=(4ac+3b)(5a^2b-7c)
3)ax^2+ay-bx^2-by+cx^2+cy=
есть два варианта решения -объединить попарно слагаемые 1и2, 3и 4, 5и 6; либо обединить 1,3,5 и 2,4,6, напишу первый вариант
a(x^2+y)-b(x^2+y)+c(x^2+y)=(x^2+y)(a-b+c)
4)x^3-x^2+x^2y+x-xy+y=(x^3-x^2+x ) + (x^2y-xy+y)=x(x^2-x+1)+y(x^2-x+1)=(x^2-x+1)(x+y)