1. log₂(x+1)<log₂(6-2x) ОДЗ: x+1>0 x>-1 6-2x>0 x<3 ⇒ x∈(-1;3)
x+1<6-2x 3x<5 x<5/3=1²/₃.
ответ: x∈(-1;1²/₃).
2.lg(x-3) >0 ОДЗ: x-3>0 x>3.
lg(x-3)>lg1 x-3>1 x>4.
ответ: x∈(4;+∞).
3. log₅((3-x)/(2-x))<1 ОДЗ: -∞__+__2__-__3__+__+∞ ⇒ x∈(-∞;2)U(3;+∞)
log₅((3-x)/(2-x))<log₅5 (3-x)/(2-x)<5 3-x<10-5x 4x<7 x<7/4=1³/₄
ответ: x∈(-∞;1³/₄).
4. log₃₃(33x+2)≤1 ОДЗ: 33x+2>0 33x>-2 x>-2/33
log₃₃(33x+2)≤log₃₃33
33x+2≤33 33x≤31 x≤31/33
ответ: x∈(-2/33;31/33].
5. log₁/₉(2x-1)+log₁/₉(x)>0 ОДЗ: 2x-1>0 x>1/2 x>0 ⇒ x>1/2=0,5
log₁/₉((2x-1)*x)>log₁/₉1
(2x-1)*x<1 2x²-x-1<0 D=9 x₁=1 x₂=-0,5 ⇒
(x-1)(x+0,5)<0 -∞__+__-0,5__-__1__+__+∞ ⇒ x∈(-0,5;1).
ответ: x∈(0,5;1).
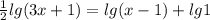
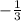, x > 1 ⇒ x > 1. 
при условии существования логарифмов. В нашем случае это тоже работает: данные логарифмы десятичные, значит, в основании 10. Вспомним, что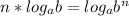 
(также при условии существования логарифма). Сразу вычислим lg1 - чтобы получить из 10 1, нужно 10 возвести в нулевую степень, значит, что 0. Тогда наше уравнение равносильно такому: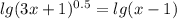 
т.к. а=1 (т.е. положительное), то ветви параболы направлены вверх
находим вершину:
х=-b/2a
x=6/2=3
y=3²-6*3+7=9-18+7=-2
(3:-2)
находим пересечение с осью Ох:
х²-6х+7=0
D=36-4*7=8
x₁=(6+√8)/2≈4.4
x²=(6-√8)/2≈1.6
(4.4;0)(1.6;)
так как у функции коэффициент с=7, то график пересекает ось Оу в точке (0;7)
строим график (в файле приложен)..
Смотрим на график:
Функция убывает на промежутке (-∞;3)
возрастает на промежутке (3;+∞)
y(-2)=(-2)²-6*(-2)+7=4+12+7=23