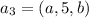- арифметическая прогрессия. Тогда: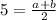
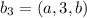- геометрическая прогрессия. Тогда: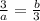
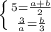
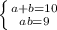
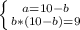
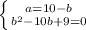
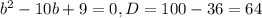
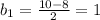
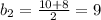
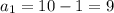
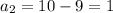
Решение.
Впишем четырехугольник ABCD в прямоугольник EFGH со сторонами,
параллельными диагоналям (EF || AC и EH || BD) - смотри рисунок.
Пусть L - точка пересечения прямых DC и EF, а M - точка на прямой HG такая, что LM || FG.
Тогда ABLC - параллелограмм, следовательно, AB = CL.
Так как GM = FL = EB = HD и AH = CG, то треуг-к AHD = треуг-ку CGM ,
следовательно, AD = CM. BC + CM = BC + AD .
Но BM = DL как диагонали прямоугольника BLDM, и DL = DC + CL = DC + AB.
Следовательно, AD + BC = DL = DC + CL = DC + AB, что и требовалось доказать.
х1=-9
По теореме Виета, х1*х2=72
-9*х2=72
х2=-8
По той же теореме, х1+х2=-р
р=-(-9-(-8))
р=-(-9+8)
р=-(-1)
р=1
ответ: х2=-8
р=1