1. да
2. нет
3. да
4. да
5. нет
6. нет
7. нет
8. нет
9.нет
Объяснение:
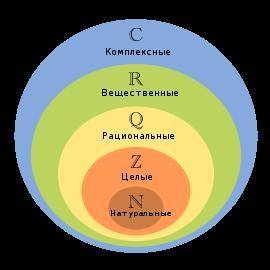
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3... и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Это конечные дроби и бесконечные периодические дроби . Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом.
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.

Y= x³ + 3*x² - 4
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет
2. Пересечение с осью Х. Y=0
При х1 = x2 = - 2, x3 = 1
3. Пересечение с осью У. У(0) = -4
4. Поведение на бесконечности.
limY(-∞) = - ∞ и limY(+∞) = +∞
Горизонтальной асимптоты - нет
5. Исследование на чётность.
Y(-x) ≠ - Y(x)
Функция ни чётная ни нечетная - общего вида..
6. Производная функции.
Y'(x)= 3*x² + 6*x = 3*x*(x+2) = 0
7. Корень при Х= - 2.
Возрастает - Х∈(-∞;-2)∪(0;+∞)
максимум - Y(-2) =0
минимум - Y(0) = - 4
Убывает - X∈(-2;0)
8. Вторая производная
Y"(x) = 6*x +6 = 6*(x+1)
9. Точка перегиба
Y"(x)=0 при X=-1
Выпуклая - Х∈(-∞;-1] Вогнутая - Х∈[-1;+∞).
10. График в приложении.