z = x*y
1. Найдем частные производные.
2. Решим систему уравнений.
y = 0
x = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 0
y = 0
Откуда y = 0
Данные значения y подставляем в выражение для x. Получаем: x = 0
Количество критических точек равно 1.
M1(0;0)
3. Найдем частные производные второго порядка.
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(0;0)
AC - B2 = -1 < 0, то глобального экстремума нет.
Вывод: Глобального экстремума нет.
Обе функции монотонно возрастающие.
Получили, что мЕньшему значению переменной соответствует мЕньшее значение функции, и наоборот, бОльшему значению переменной соответствует бОльшее значение функции. Значит функция возрастающая .
Знак выражения получили (+) , так как произведение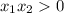 в силу того, что гиперболу рассматриваем на двух промежутках при
в силу того, что гиперболу рассматриваем на двух промежутках при 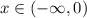 и при
и при 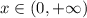 , где
, где 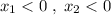 и
и 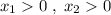 .
.
Получили, что бОльшему значению переменной соответствует бОльшему значение функции, и наоборот, мЕньшему значению переменной соответствует мЕньшему значение функции. Значит функция возрастающая .