![\left \{ {{sin(x)+cos(y)=\frac{1}{2}} \atop {sin(y)-cos(x)=\frac{1}{2}}} \right. \\\\ \left \{ {{sin(x)+cos(y)-[sin(y)-cos(x)]=\frac{1}{2}-\frac{1}{2}} \atop {sin(y)-cos(x)=\frac{1}{2}}} \right. \\\\ \left \{ {{[sin(x)+cos(x)]-[sin(y)-cos(y)]=0} \atop {sin(y)-cos(x)=\frac{1}{2}}} \right. \\\\ \left \{ {{\sqrt{2}sin(x+\frac{\pi}{4})-\sqrt{2}sin(y-\frac{\pi}{4})=0} \atop {sin(y)-cos(x)=\frac{1}{2}}} \right. \\\\](/tpl/images/0904/0882/79253.png)
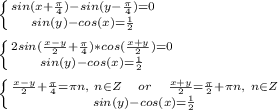
![\left \{ {{x-y=-\frac{\pi}{2}+2\pi n,\ n\in Z\ \ \ or\ \ \ x+y=\pi+2\pi n,\ n\in Z} \atop {sin(y)-cos(x)=\frac{1}{2}}} \right. \\\\ \left \{ {{y=x+\frac{\pi}{2}-2\pi n,\ n\in Z\ \ \ or\ \ \ y=-x+\pi+2\pi n,\ n\in Z} \atop {sin(y)-cos(x)=\frac{1}{2}}} \right. \\\\ \left \{ {{y=x+\frac{\pi}{2}-2\pi n,\ n\in Z} \atop {sin[x+\frac{\pi}{2}-2\pi n]-cos(x)=\frac{1}{2}}} \right.\ or\ \left \{ {{y=-x+\pi+2\pi n,\ n\in Z} \atop {sin(-x+\pi+2\pi n)-cos(x)=\frac{1}{2}}} \right. \\\\](/tpl/images/0904/0882/4fe3b.png)
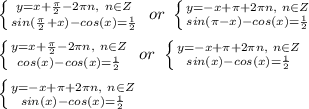
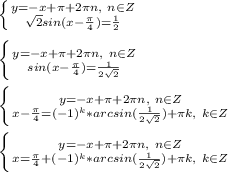
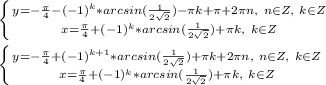
Рассмотрим несколько случаем. На месте четной цифры мы будем писать Ч, на месте нечетной - Н. Тот факт, что число нечетное, означает, что последняя цифра у числа нечетная.
1) Число имеет вид ЧЧН. Поскольку на первом месте не может стоять 0, на первое место претендуют 3 цифры - 2, 4, 6. На второе место претендуют 4 цифры - 0, 2, 4, 6 (а если цифры не должны повторяться, то 3 цифры). На третье место претендуют 4 цифры - 3, 5, 7, 9.
Всего получается 3·4·4=48 чисел (при второй интерпретации условия 3·3·4=36 чисел).
2) ЧНН. Здесь аналогично получается 3·4·4=48 чисел (или 3·4·3=36).
3) НЧН. Здесь 4·4·4=64 чисел (или 4·4·3=48).
4) ННН. Здесь 4·4·4=64 числа (или 4·3·2=24)
Суммарно получаем 48+48+64+64=224 чисел - если повторения цифр допускаются (или 36+36+48+24= 144 чисел если все цифры должны быть разные).
Замечание. Если цифры могут совпадать, задачу можно сделать проще . На первом место может стоять любая из цифр, кроме 0 - всего 7 вариантов. На втором месте может стоять любая цифра - всего 8 вариантов. На третьем месте может стоять любая из нечетная цифра - 4 варианта. Всего получаем 7·8·4=224 числа.
ответ: 224 чисел, в которых возможно совпадение цифр, и 144 числа, в которых все цифры разные.
Рассмотрим несколько случаем. На месте четной цифры мы будем писать Ч, на месте нечетной - Н. Тот факт, что число нечетное, означает, что последняя цифра у числа нечетная.
1) Число имеет вид ЧЧН. Поскольку на первом месте не может стоять 0, на первое место претендуют 3 цифры - 2, 4, 6. На второе место претендуют 4 цифры - 0, 2, 4, 6 (а если цифры не должны повторяться, то 3 цифры). На третье место претендуют 4 цифры - 3, 5, 7, 9.
Всего получается 3·4·4=48 чисел (при второй интерпретации условия 3·3·4=36 чисел).
2) ЧНН. Здесь аналогично получается 3·4·4=48 чисел (или 3·4·3=36).
3) НЧН. Здесь 4·4·4=64 чисел (или 4·4·3=48).
4) ННН. Здесь 4·4·4=64 числа (или 4·3·2=24)
Суммарно получаем 48+48+64+64=224 чисел - если повторения цифр допускаются (или 36+36+48+24= 144 чисел если все цифры должны быть разные).
Замечание. Если цифры могут совпадать, задачу можно сделать проще . На первом место может стоять любая из цифр, кроме 0 - всего 7 вариантов. На втором месте может стоять любая цифра - всего 8 вариантов. На третьем месте может стоять любая из нечетная цифра - 4 варианта. Всего получаем 7·8·4=224 числа.
ответ: 224 чисел, в которых возможно совпадение цифр, и 144 числа, в которых все цифры разные.