1) Логарифм определен на положительной полуоси, на ней х не равен нулю, так что со знаменателем все ок. Потому функция определена на положительной полуоси (0,+беск)
2) Фцнкция не определена на отрицателных значениях, потому она не может быть четной или нечетной.
3)С Оу не пересекается, т.к не определена в точке х=0. С Ох точка пересечения - решение уравнения
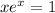
это уравнение не имеет решений в элементарных функциях, это далеко за рамками школьной программы. Если устроит - решение этого уравнения - так называемая константа Омега.
4) Функция непрерывна на (0,+беск) как сумма константы и частного двух непрерывных функций
5)---
6)Асимптоты 2, видно из самого графика. Одна - у=1, так как функция стркмится к 1 при х стремящемуся к бесконечности. Вторая - х=0, так как функция стрмится к минус бесконечности при х стремящимуся к нулю. Возможно, в вашем курсе вторая асимптота не рассматривается, так как асимптота х=0 не есть функция.
7,8) Так как
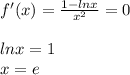
То х=е - точка экстремума. Уже говорилось, что функция стремится к 1 при х стремящемуся к бесконечности и к -беск при х стрмящемуся к нулю. Так как в точке е функция больше 1, то это точка локального (и глобального) максимума.
Функция растет на (0,е) и падает на (е, +беск)
9)
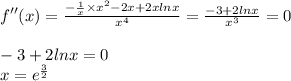
Для иксов меньше найенного значения вторая производная отрицательна, следовательно функция выпукла. Для иксов больше - чсе наоборот, следтвательно, функция вогнута