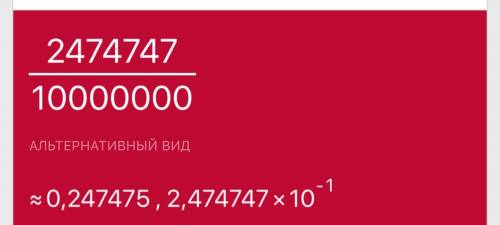
ответ:
y' = 4x^3-4x
приравниваем ее к нулю:
4x^3-4x = 0
x1 = 0
x2 = -1
x3 = 1
вычисляем значения функции
f(0) = 8
f(-1) = 7
f(1) = 7
fmin = 7, fmax = 8
используем достаточное условие экстремума функции одной переменной. найдем вторую производную:
y'' = 12x^2-4
вычисляем:
y''(0) = -4< 0 - значит точка x = 0 точка максимума функции.
y''(-1) = 8> 0 - значит точка x = -1 точка минимума функции.
y''(1) = 8> 0 - значит точка x = 1 точка минимума функции.
объяснение:
ассмотрим ситуацию с извлечением двух шариков для игры и последующим возвратом. Возможно 4 случая:
1. С вероятностью 1/4 извлечены были старый и старый шарик
2. С вероятностью 1/4 извлечены были новый и новый шарик
3. С вероятностью 1/4 извлечены были старый и новый шарик
4. С вероятностью 1/4 извлечены были новый и старый шарик
Поскольку нас не интересует порядок извлечения шаров, то последние две ситуации можно объединить в одну следующим образом:
3. С вероятностью 1/2 в некотором порядке были извлечены старый и новый шарик.
В первом случае число старых и новых шариков не изменилось: 6 новых и 4 старых.
Во втором случае пара новых шариков теперь стали игранными: осталось 4 новых шарика, соответственно старых 6.
В третьем случае один новый шарик теперь стал игранным: осталось 5 новых шариков, соответственно старых 5.
Общее число шариков не изменялось - 10 штук.
1. Вероятность вытащить из 6 новых и 4 старых шариков 2 новых:
2. Вероятность вытащить из 4 новых и 6 старых шариков 2 новых:
3. Вероятность вытащить из 5 новых и 5 старых шариков 2 новых:
Учитывая тот факт, что каждый случай также наступает с определенной вероятностью, а также что все эти случаи несовместны, получим: