В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
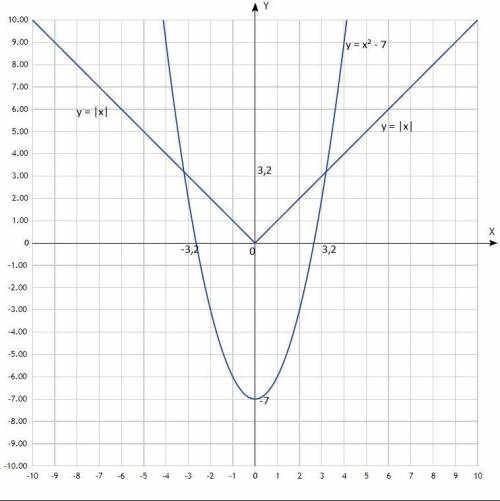
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).
В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).

(y+3)²=y²+6y+9;
(a-5)²=a²-10a+25;
(2b²-1)²=4b^4-4b²+1;
(5+3c²)²=9c^4+30c^2+25;
(c+2)(c²-c+4)=c^3+8;
(y-3)(y²+3y+9)=y^3-27.