Question

Указать верное утверждение. а. любая арифметическая прогрессия может быть задана формулой вида : an = kn + b б. разность арифметической прогрессии (d) равна разности предыдущего и последующего членов: d = an - an+1 в. каждый член арифметической прогрессии равен среднему арифметическому двух последующих членов прогрессии

Answer 1

A) Верно, так как это теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа.

Теорема. Любая арифметическая прогрессия (аn) может быть задана формулой an = kn + b, где k и b - некоторые числа; также имеет место обратное утверждение, если последовательность (аn) задана формулой an = kn + b, где k и b - некоторые числа, то эта последовательность является арифметической прогрессией.

Б) Не верно. Верна формула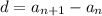 $d=a_{n+1}-a_n$

В) Неверно. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:

                      $a_n=\dfrac{a_{n-1}+a_{n+1}}{2}$