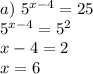
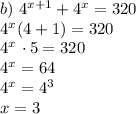
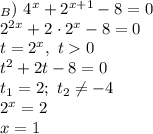
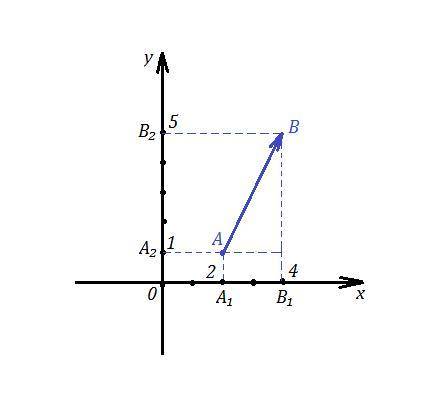
Необходимо начертить вектор АВ=(2;4) . Начало вектора выбрать произвольно.
Координаты вектора - это проекции вектора на оси ОХ и ОУ. То есть вектор АВ проектируется на ось ОХ в отрезок , длина которого равна 2 единицам, а на ось ОУ - в отрезок, длина которого 4 единицы. Причём, так как координаты положительные, то направление от проекции начала вектора к проекции конца вектора такое же, как и у осей координат.
Если , например, за начало вектора возьмём точку А(2,1), то от точки А₁(2,0) , которая является проекцией точки А на ось ОХ, отложим вдоль оси ОХ отрезок длиной 2 единицы в направлении оси ОХ, попадём в точку В₁(4,0), которая будет проекцией точки В на ось ОХ. А₁В₁ - проекция вектора АВ на ось ОХ.
Аналогично, от точки А₂(0,1) отложим вдоль оси ОУ отрезок длиной 4 единицы, попадём в точку В₂(0,5) . А₂В₂ - проекция вектора АВ на ось ОУ.
Затем соединим точку А(2,1) с точкой В(4,5), получим искомый вектор АВ=(2,4).
Тангенс угла наклона касательной равен производной в точке касания к графику функции.
tgα = y'(x).
1) y = 0,2x^2 + 2x - 4, A(2; 0,8).
Проверяем - принадлежит ли точка данной функции.
0,2*2² + 2*2 - 4 = 0,8. Да, принадлежит.
Находим производную: y' = 0,2*2x + 2.
y'(2) = 0,2*2*2 + 2 = 2,8.
ответ: tgα = 2,8.
2) y = -3x^2 - x + 5, А(-2; -5).
Аналогично проверяем - точка А на кривой (парабола).
y' = -6x - 1,
y'(-2) = -6*(-2) - 1 = 12 - 1 = 11.
ответ: tgα = 11.
3) y = (x^2 - 1)/(x - 5), A(3; 3 2/3). (Ели так дано задание)
В этой задаче сложное решение, так как точка А не лежит на кривой.
Производная : y' = (2x(x - 5) - 1*(x^2 - 1))/(x - 5)^2) = (x^2 - 10x + 1)/((x - 5)^2).
Производная в точке касания хо: (xо^2 - 10xо + 1)/((xо- 5)^2).
Получим уравнение касательной проходящей через точку A(3;3 2/3):
3 2/3 = ((xо^2 - 10xо + 1)/((xо- 5)^2))(3 - хо) + ((xо^2 - 1)/(xо - 5)).
Решение затруднено, так функция - кубическая.
Ориентировочно решение найдено графически в программе ГеоГебра: у = -18,76х + 59,95.
График приведен во вложении.