Сам график не построю, но всё, что нужно для его построения, напишу
Сначала нужно выразить одну переменную через другую:
y - 6x = -25
y = 6x - 25
-y - x = -5
y = 5 - x
Данные функции являются линейными, поэтому их графиками будут прямые, для построения графиков этих функций нужно подставить значение x, и найти при данном значении x значение y (Т.е., к примеру в первой функции при x = 1, y = 6 * 1 - 25 = -19):
y = 6x - 25
Координаты:
x = 1 y = -19
x = 0 y = -25
Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек
То же самое делаешь и со второй функцией:
y = 5 - x
Координаты:
x = 0 y = 5
x = 1 y = 4
Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек
Данные прямые пересекутся, и точка их пересечения будет решением системы уравнений
ответом будет 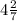 и
и 
В связи с таким ответом вопрос: ты точно всё правильно написал?
первое число дает остаток 1 при делении на 4
значит куб первого числа при делении на 4 даст такой же остаток как и 1 в кубе, т.е как число 1*1*1=1
число 1 при делении на 4 дает остаток 1
итого куб первого числа при делении на 4 даст остаток 1
второе число дает остаток 3 при делении на 4
значит куб второго числа при делении на 4 даст такой же остаток как и 3 в кубе, т.е. как число 3*3*3=27
число 27 при делении на 4 дает остаток 3
сумма кубов первого и второго чисел при делении на 4 даст такой же остаток какой даст при делении на 4 сумма остатков чисел при делении на 4, т.е. как число 1+3=4,
так как 4 при делении на 4 дает остаток 0, то
сумма кубов этих чисел кратна 4
----------------------------------
второй
так как первое число при делении на 4 дает остаток 1, то его можно записать в виде 4n+1, где n - некоторое целое число
аналогично второе можно записать в виде 4k+3, где k - некоторое целое число
сумма кубов этих чисел
а значит сумма кубов делится нацело на 4. Доказано