Количество игр: 2
:
Выигрыш (В) - 3 очка
Ничья (Н) - 1 очко
Проигрыш (П) - 0 очков
P(Н) = 0,1
Так как общая вероятность равна 1 или 100%, то:
P(В+П) = 1 - 0,1 = 0,9
По условию Р(В) = Р(П), тогда:
Р(В) = P(В+П) /2 = 0,9 / 2 = 0, 45
Р(П) = P(В+П) /2 = 0,9 / 2 = 0, 45
Команде не удасться выйти в следующий круг соревнований при следующих событиях:
1 игра - проигрыш, 2 игра - выигрыш1 игра - выигрыш, 2 игра - проигрыш1 игра - проигрыш, 2 игра - проигрыш1 игра - ничья, 2 игра - ничья1 игра - ничья, 2 игра - проигрыш1 игра - проигрыш, 2 игра - ничьяР(1) = Р(П) * Р(В) = 0,45 * 0,45 = 0,2025
Р(2) = Р(В) * Р(П) = 0,45 * 0,45 = 0,2025
Р(3) = Р(П) * Р(П) = 0,45 * 0,45 = 0,2025
Р(4) = Р(Н) * Р(Н) = 0,1 * 0,1 = 0,01
Р(5) = Р(Н) * Р(П) = 0,1 * 0,45 = 0,045
Р(6) = Р(П) * Р(Н) = 0,45 * 0,1 = 0,045
Вероятность того, что команде не удастся выйти в следующий круг соревнований:
Р = Р(1) + Р(2) + Р(3) + Р(4) + Р(5) + Р(6) = 0,2025 + 0,2025 + 0,2025 + 0,01 + 0,045 + 0,045 = 0,7075 = 0,71
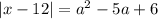
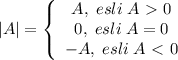
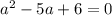 при
при 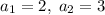 .
.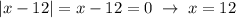 .
.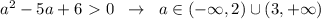
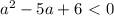 , то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае
, то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае 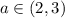 .
.
Чтобы найти диагональ прямоугольника, нам необходимо знать его стороны. Найдем их. Пусть одна сторона а см, а другая b см. Тогда:
S=a*b=60
a-b=7
Решим систему уравнений:
a*b=60 (b+7)*b=60 b²+7b-60=0
a-b=7 a=b+7 a=b+7
Решим квадр.уравнение b²+7b-60=0 D=289 b1=(-7-√289)/2
b2=(-7+√289)/2
b1 не подходит, т.к. b1<0
a=(-7+√289)/2+7=(7+√289)/2
Диагональ равна:
d²=a²+b²=((7+√289)/2)²+((-7+√289)/2)²=49/4+(7√289)/2+289/4+49/4-(7√289)/2+289/4=676/4=169
d=√169=13 (см)