Пусть Х1, Х2 ... Xn - выборка независимых случайных величин.
Упорядочим эти величины по возрастанию, иными словами, построим вариационный ряд:
Х(1) < Х(2) < ... < X (n) , (*)
где Х(1) = min ( Х1, Х2 ... Xn),
Х(n) = max ( Х1, Х2 ... Xn).
Элементы вариационного ряда (*) называются порядковыми статистиками.
Величины d(i) = X(i+1) - X(i) называются спейсингами или расстояниями между порядковыми статистиками.
Размахом выборки называется величина
R = X(n) - X(1)
Иными словами, размах это расстояние между максимальным и минимальным членом вариационного ряда.
Выборочное среднее равно: = (Х1 + Х2 + ... + Xn) /
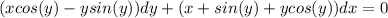
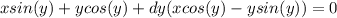
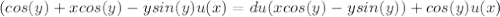
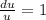
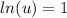
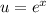
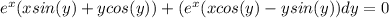
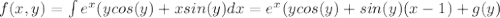 ;
;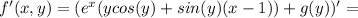
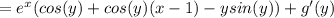
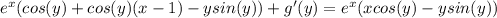
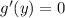
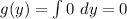
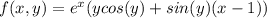
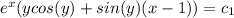
2)11-в(в квадрате)=(√11-в)(√11+в)
3)m-100=(√m-10)(√m+10)