По условию-
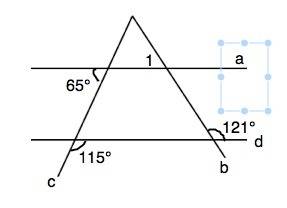
при пересечении прямых а и d секущей с тупой угол, образованный при пересечении прямых d и с равен 115°, а острый угол, образованный пересечением прямых а и с, равен 65°.
Угол, смежный этому углу, равен 180°-65°=115°. Он равен соответственному ему углу. По свойству углов, образующихся при пересечении параллельных прямых секущей, прямые а и d – параллельны. ⇒
Угол 1 равен соответственному ему углу, смежному с углом, градусная мера которого при пересечении прямых а и d секущей b равна 121°
Угол 1=180°-121°=59°
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Графики функций, представленных слева и справа в неравенстве пересекаются при х = -1 (см. вложение). График находится ниже графика прямой у = 2х+5 на промежутке
находится ниже графика прямой у = 2х+5 на промежутке 
Значит решением данного неравенства является промежуток .
.