Боюь, что и у меня не сойдется с ответом, но хочу предложить следующую модель:
Заменим однородную палочку невесомым стержнем, на концах которого находятся шарики одной массы (в сумме - масса палочки).
Оси Х и У направим как и обычно. Они буду обозначать пол и стену.
Нарисуем чертеж для какого-то произвольного положения системы шаров. Нижний шар в точке с абсциссой х, верхний в точке с ординатой у . Острый угол между стержнем и осью х назовем а.
Со стороны стержня на шары действует равная по модулю сила F, линия действия которой совпадает с линией стержня, а направления - соответственно - в пол под углом а, и в стену под углом (90-а). Для шара находящегося на полу, проекция этой силы на ось Х и является причиной движения. А для шара находящегося наверху проекция этой силы на ось У ,наоборот, препятствует движению под действием силы тяжести.
Уравнения Ньютона в проекциях на ось Х для нижнего шара, и в проекциях на ось У - для верхнего шара:
-ускорение нижнего шара.
- ускорение верхнего шара
Кинематические уравнения равноускоренного движения нижнего шара с нулевой начальной скоростью:
Отсюда получим:
Как я понимаю, последняя формула является ключевой. Теперь мы знаем,через сколько секунд нижний конец палочки был в координате х и имел скорость .
Теперь:
(1)
Подставим (1) в уравнение динамики второго(верхнего) шара и получим:
Теперь подставив данные, с учетом того что tga = 36/48=0,75 (легко посчитать самому), получим удручающий ответ. Оставляю его таким - в общем виде. Не знаю, где ошибаюсь.
В первый день. Каждый брошеный кубик охлаждает налившуюся за 6 сек воду массой m1 до приемлемой температуры.
Во второй день. Каждый брошеный кубик охлаждает налившуюся за время x воду массой m2 до приемлемой температуры.
Мы не будем вдаваться, как кубик тает и нагревается, важно, что, тая и нагреваясь до 35 он поглощает одно и то же количество теплоты Q
Тепловой баланс в первый день и второй день
То есть, масса воды, которая должна наливаться между бросками во второй день составляет 5/6 массы воды, которая наливалась в 1-й день. Так как кран открыт одинаково в оба дни, мы понимаем, что если в 1-й день бросок происходил раз в 6 сек, во второй день должен быть один бросок в 6*5/6 = 5 секунд
Боюь, что и у меня не сойдется с ответом, но хочу предложить следующую модель:
Заменим однородную палочку невесомым стержнем, на концах которого находятся шарики одной массы (в сумме - масса палочки).
Оси Х и У направим как и обычно. Они буду обозначать пол и стену.
Нарисуем чертеж для какого-то произвольного положения системы шаров. Нижний шар в точке с абсциссой х, верхний в точке с ординатой у . Острый угол между стержнем и осью х назовем а.
Со стороны стержня на шары действует равная по модулю сила F, линия действия которой совпадает с линией стержня, а направления - соответственно - в пол под углом а, и в стену под углом (90-а). Для шара находящегося на полу, проекция этой силы на ось Х и является причиной движения. А для шара находящегося наверху проекция этой силы на ось У ,наоборот, препятствует движению под действием силы тяжести.
Уравнения Ньютона в проекциях на ось Х для нижнего шара, и в проекциях на ось У - для верхнего шара:
Кинематические уравнения равноускоренного движения нижнего шара с нулевой начальной скоростью:
Отсюда получим: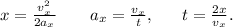
Как я понимаю, последняя формула является ключевой. Теперь мы знаем,через сколько секунд нижний конец палочки был в координате х и имел скорость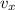 .
.
Теперь:
Подставим (1) в уравнение динамики второго(верхнего) шара и получим:
Теперь подставив данные, с учетом того что tga = 36/48=0,75 (легко посчитать самому), получим удручающий ответ. Оставляю его таким - в общем виде. Не знаю, где ошибаюсь.