не совсем краткий но конспект библиотека
материалов ДОБАВИТЬ В ИЗБРАННОЕ
СКОРОСТЬ. ЕДИНИЦЫ СКОРОСТИ.
ЦЕЛЬ УРОКА. Дать понятие об основной кинематической характеристике прямолинейного движения-скорости. Познакомить учащихся с понятием средней скорости и на примере показать, как она вычисляется.
СОДЕРЖАНИЕ ОПРОСА.
По каким признакам мы судим, что тело находится в движении?
Какие вы знаете виды движений?
Приведите примеры.
Каковы признаки равномерного движения?
Приведите примеры равномерных движений.
Каковы признаки неравномерного движения?
Приведите примеры.
Основной материал.
Понятие скорости. Единицы скорости. Формула для расчета скорости равномерного движения. Графическое изображение скорости. Понятие средней скорости неравномерного движения. Как определяется средняя скорость? Сравнение скоростей движения различных тел, света, звука (таблица учебника).
ДЕМОНСТРАЦИИ.
Сравнение двух равномерных движений.
Движение шарика по наклонному желобу - пример неравномерного движения.
Движение заводного автомобиля. Определить путь, пройденный им за 5 секунд, найти среднюю скорость движения.
НОВЫЙ МАТЕРИАЛ.
После повторения материала демонстрируем опыт по сравнению двух равномерных движений, например по движению пузырьков воздуха в стеклянных трубках одинакового сечения, одна из которых заполнена водой, а вторая маслом, или по движению тележки с капельницей. На основании опытов подводим учащихся к выводу, что равномерные движения отличаются друг от друга особым качеством. Сообщаем, что в физике для характеристики этого качества введена особая физическая величина, называемая скоростью. Подчеркиваем, что скорость – физическая величина, характеризующая движение тела. Скорость – быстрота движения.
На конкретном примере показываем, что о скорости тела нельзя судить ни по пройденному пути, ни по времени движения. Для того чтобы судить о скорости тела, надо одновременно знать пройденный путь и время движения.
Определения. Скорость при равномерном движении тела показывает, какой путь тело в единицу времени.
Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени разделить на этот промежуток времени.
Скорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое этот путь пройден.
Единицы измерения: км/ч; м/с. В Международной системе (СИ) скорость измеряют в метрах на секунду. Это значит, что за единицу скорости принимается скорость такого равномерного движения, при котором за 1 секунду тело проходит путь, равный 1 метру.
На примерах надо показать, что одну и ту же величину скорости можно выразить в различных единицах.
36км/ч = 10м/с
На примере показываем, что для определения движения тела недостаточно знать величину пути, пройденного телом, и величину его скорости. Необходимо знать еще и направление скорости, которое на чертежах изображается отрезком прямой в определенном масштабе со стрелкой на конце. Здесь же изобразим графически скорость автомобиля. Вводим понятие о том, что скорость является векторной величиной.
Затем решим несколько задач на определение скорости равномерного движения.
Задача.№1.
Дано: Решение:
=900м 1)Вычислим скорость плота.
t=20мин=1200с U= /t U=
U-?
ОПЫТ. По наклонному желобу вниз движется шарик. Предлагаем учащимся определить, какое это движение. Отсчет времени ведем по метроному. Измерив пути, пройденные шариком за одинаковые промежутки времени, устанавливаем, что это движение является неравномерным. Предлагаем учащимся привести примеры неравномерных движений. Примеры дополняем опытами по движению шарика вверх по наклонному желобу, движению заводной игрушки. Затем рассматриваем примеры из учебника. Рассмотрим движение двух автомобилей. На стойке на одной оси укреплены деревянный диск и эллипс с окружностями одинаковой длины. К ним прикреплены концы нитей одинаковой длины. К другим концам привязаны два автомобиля, которые находятся на одинаковом расстоянии от оси вращения. При вращении оси автомобили движутся – первый неравномерно, а второй равномерно. За время одного оборота проходят равные пути. Следовательно, средняя скорость неравномерного движения первого автомобиля равна скорости второго автомобиля, который движется равномерно.
В практике мы редко имеем дело с равномерным движением, поэтому почти всегда пользуемся понятием средней скорости. Она обычно приводится и в таблицах скоростей.
ЗАДАЧА №2.
Велосипедист проехал 200м за 20с, последующие 450м за 30с и последние 70м за 10с. Определите среднюю скорость велосипедиста.
ЗАДАЧА №3.
Первую половину пути, равную 1500м, конькобежец бежал со скоростью 6м/с, а вторую – 12м/с. С какой средней скоростью бежал конькобежец?
Обращаем внимание учащихся на то, что средняя скорость движения на всем пути не является средней арифметической скоростей на отдельных участках.
ЗАДАЧА №4.
Определить скорость автомобиля, если за 2 часа он путь 144км.
ЗАДАЧА №5.
Какая скорость больше: 108км/ч или 30м/с?
УПРАЖНЕНИЕ 4(3,2).
k = 196 Н/м.
Объяснение:
Дано: m = 0,02 кг; h = 5 м; x = 0,1 м.
Знайти: k.
Розв’язок. Розглянемо систему «пружина – куля». Оскільки на тіла системи діють тільки консервативні сили, то для розв’язку задачі можна застосувати закон збереження енергії в механіці. Відповідно до нього, повна механічна енергія E1 системи в початковому стані (у даному випадку перед пострілом) дорівнює повній енергії E2 у кінцевому стані (коли куля піднялася на висоту h), тобто E1 = E2, або
T1 + W1= T2 + W2, (1)
де T1, T2, W1 іW2 – кінетичні і потенційні енергії системи у початковому і кінцевому станах. Оскільки кінетичні енергії кулі у початковому і кінцевому станах дорівнюють нулеві, то рівність (1) набуває виду
W1 = W2, (2)
Приймемо, що потенціальна енергія кулі в полі сил тяжіння Землі, знаходячись в стані спокою на стиснутій пружині, дорівнює нулю, а висоту підйому кулі будемо відраховувати від торця стиснутої пружини. Тоді енергія системи у початковому стані буде дорівнювати потенціальній енергії стиснутої пружини, тобто , а в кінцевому стані – потенціальній енергії кулі на висоті h, тобто W2 = mgh.
Підставивши виразW1 іW2 у формулу (2), знайдемо
. (3)
k = 2·0,02·9,81·5/(0,1) = 196 Н/м.
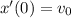 .
.
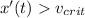 .
.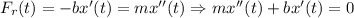
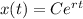 . Тогда дифференциальное уравнение имеет вид
. Тогда дифференциальное уравнение имеет вид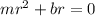
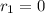
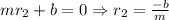
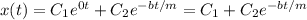
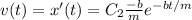
 ,
, 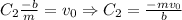 .
.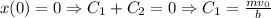
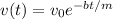
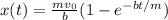
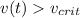 , то есть
, то есть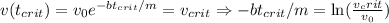
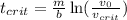
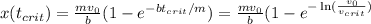
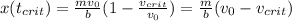
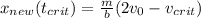
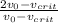 ,
,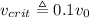 , это отношение равно
, это отношение равно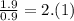 .
.
Скорость – это физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло. Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по траектории движения.
Единицы измерения скорости
Линейная скорость: Метр в секунду, (м/с), производная единица системы СИ Километр в час, (км/ч)
Объяснение: