Решите задачи, не забывайте правильно все оформить (дано, решение...). Домашнюю работу выполняете в тетради для домашних работ.
1. Из ствола орудия, масса которого 800 кг, вылетает снаряд со скоростью
600 м/с. Какова масса снаряда, если скорость отдачи орудия в
противоположную сторону
— 10 м/с?
2. С неподвижной тележки массой 30 КГ, совершен прыжок. Какую скорость
приобретет тележка, если скорость прыгуна 3 м/с, а его масса 60 кг? Прыжок
был сделан в горизонтальном направлении.
3. Фигурист, стоя на коньках на льду, бросил вперед кусок льда массой 8 кг
со скоростью 3 м/с. Найдите массу фигуриста, если в момент броска он
откатился назад со скоростью 40 см/с
ok
 тогда мы можем выразить время, которое тратит жук на прохождение расстояния между
тогда мы можем выразить время, которое тратит жук на прохождение расстояния между 
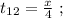
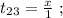
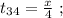


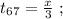
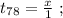

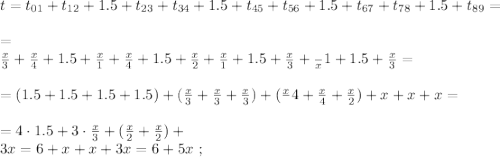


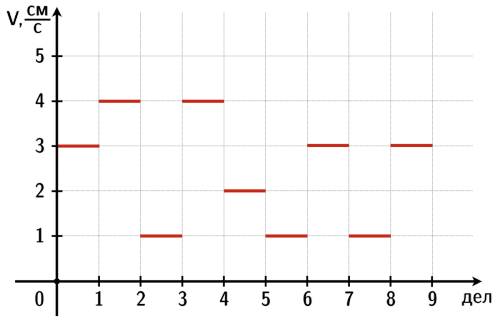
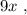 поскольку мы изначальнго определили
поскольку мы изначальнго определили  как цену деления линейки Глюка. Стало быть:
как цену деления линейки Глюка. Стало быть:
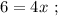
 см
см