А 12,5 км/ч
Объяснение:
30 км : 10 км/ч =3 часа (велосипедист ехал первый отрезок пути)
20 км : 20 км/ч =1 час (велосипедист ехал второй отрезок пути)
30 км + 20 км = 50 км (велосипедист проехал за весь путь)
3 часа + 1 час = 4 часа (велосипедист ехал всего)
50 км : 4 часа = 12,5 км/ч (средняя скорость велосипедиста)
12. Δx=8 см
16. Δx= 12 см
Объяснение:
12.
F=k*Δx
Δx=F/k=4/50=0.08 м = 8 см
16.
F=k*Δx
Δx=F/k=12/100=0.12 м = 12 см
15.
Второй закон Ньютона в векторной форме
Fрез(вектор)=ma(вектор)
F(вектор)+mg(вектор)=ma(вектор)
В проекции на ось совпадающей с направлением движения, то есть направленной вниз
F+mg=ma
F=-Fупр=k*дельтаХ
k*ΔХ+mg=ma
а=(k*ΔХ+mg)/m=29.8 м/с2
ΔХ=F/k=0,2 м
то есть мы м с ускорением 29,8 м/с2, определим максимальную скорость в конце пути
S=a*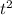
/2
t=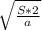
=0.116 с время когда мы набрали мак скорость
v=a*t=29.8*0.116=3.45 м/с
Объяснение:
Рисунок к задаче дополнен расчетами - в приложении.
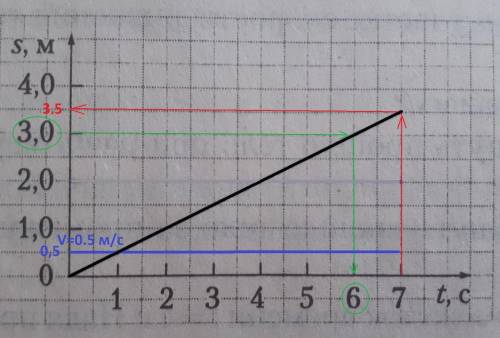
График пути - прямая линия - равномерное движение S = V*t
So = 0 - начального пути - нет.
Время движения по шкале t = 7 c
Скорость определим по формуле: V = S/t
Из точки по оси времени t = 7 проводим до пересечения с графиком пути и от него проводим на ось пути S и получаем ... S = 3.5 м.
V = 3.5 : 7 = 0.5 м/с - скорость постоянная - ответ.
Этим расчетом мы получили ответ и на второй вопрос.
Путь за 7 с равен S = 3,5 м - полный путь - ответ
Определение времени для пути S = 3 м делаем в противоположном направлении. От S = 3 м проводим горизонтальную прямую до графика пути и далее вниз до пересечения с осью времени
t(3) = 6 c - время на 3 м - ответ.
12.5 км/ч, то есть ответ А
Объяснение:
t1=S1/V1=30/10=3 ч
t2=S2/V2=20/20=1ч
Vср=S/t=(S1+S2)/(t1+t2)=50/4=12,5 км/ч