Камень подбросили с высоты 2 метров от поверхности земли вертикально вверх на 9 метров над колодцем. Затем он упал в колодец, глубина которого – 12 метров. Изобразите траекторию движения согласно данным указаниям. Определите путь и перемещение камня.

👇

Увидеть ответ

Ответ:

vadiЬПФН

08.11.2022

Объяснение:

Правильный

Камень подбросили с высоты 2 метров от поверхности земли вертикально вверх на 9 метров над колодцем.

4,6(6 оценок)

Открыть все ответы

Ответ:

бооой

08.11.2022

Клевая задача. Максимальная скорость будет в итоге складываться из вертикальной и горизонтальной компонент:
$v= \sqrt{v_y^2+v_x^2}$

Поскольку падение происходит в гравитационном поле, то вертикальная компонента не связана с параметрами капли и зависит только от высоты падения и напряженности поля (ускорения свободного падения), так что с ней все ясно:
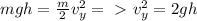
$mgh=\frac{m}{2}v_y^2 =\ \textgreater \ v_y^2=2gh$

Горизонтальная же компонента зависит от силы расталкивания двух частей одной капли. Скорость, приобретенная половинками исходной капли, полностью определит их кинетическую энергию. А по закону сохранения энергии, вся запасенная электростатическая энергия капли разделится между двумя капельками: частично станет их электростатической энергией и частично перейдет в кинетическую (по горизонтальной составляющей скорости). А значит, нам надо найти разность начальной и конечной электростатической энергии. Вот и все.

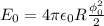
Начальная энергия капли равна $E_0=4\pi\epsilon_0 R\frac{\phi_0^2}{2}$

После разделения капли на две одинаковые их объемчики будут равны половине объема исходной капли, а отсюда находим их радиусы

:
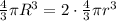
$\frac{4}{3}\pi R^3=2\cdot \frac{4}{3}\pi r^3$
$r=\frac{R}{ \sqrt[3]{2} }$

Энергия распределится поровну, поэтому суммарная электростатическая энергия двух новых капель составит:
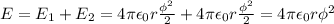
$E=E_1+E_2=4\pi\epsilon_0 r\frac{\phi^2}{2}+4\pi\epsilon_0 r\frac{\phi^2}{2}=4\pi\epsilon_0 r\phi^2$

Потенциал маленькой капли зависит от ее заряда и радиуса. Как изменился радиус мы уже знаем, а вот заряд после разделения распределился пополам - части ведь одинаковые. Поэтому
$\phi=\frac{1}{2}\frac{R}{r}\phi_0= \frac{ \sqrt[3]{2} }{2} \phi_0$

Таким образом, кинетическая энергия, связанная с горизонтальной компонентой скорости, равна
$E_k=\frac{m}{2}v_x^2=E_0-E=4\pi\epsilon_0 R\frac{\phi_0^2}{2}-4\pi\epsilon_0 r\phi^2=4\pi\epsilon_0(R\frac{\phi_0^2}{2}-\frac{R}{ \sqrt[3]{2} }\frac{ (\sqrt[3]{2})^2 }{4}\phi_0^2)$

$E_0-E=4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})$

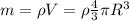$m=\rho V=\rho \frac{4}{3}\pi R^3$ - суммарная масса двух частей, разумеется равна массе исходной капли.

Отсюда
$v_x^2=\frac{2}{\rho \frac{4}{3}\pi R^3}4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})=\frac{6}{\rho R^2}\epsilon_0\phi_0^2(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})$

$v_x^2=\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})$

Окончательно,
$v= \sqrt{v_y^2+v_x^2} = \sqrt{2gh+\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})}$

4,6(35 оценок)

Ответ:

Djrktxf

08.11.2022

Мощность электрического тока:

P = U·I, где U - напряжение на нагрузке, В

I - сила тока в цепи, А

Тогда при I₁ = 4·I

P₁ = U · 4·I = 4·U·I = 4·P

Если рассмотреть подробнее:

Сила тока в цепи при неизменном напряжении будет возрастать только при уменьшении сопротивления цепи (например, при подключении параллельно дополнительной нагрузки). В этом случае:

I = U/R => I₁ = U/R₁ = U/(R:4) = 4 U/R = 4·I

То есть, во сколько раз уменьшится сопротивление, во столько же раз увеличится сила тока и, следовательно, мощность электрического тока.

ответ: при увеличении силы тока в 4 раза и неизменном

напряжении мощность тока в цепи также

возрастет в 4 раза.

4,4(81 оценок)

Это интересно:

27.06.2021

Как заставить людей в школе считать, что вы русалка?...

Образование-и-коммуникации

06.10.2021

Как решать кубические уравнения: подробное руководство...