Rab=((1/R1+1/R2)^-1)+((1/R3+1/R4)^-1)+R5=6+12+6=24 (Ом)
Iab=I1+I2=I3+I4=I5=Uab/Rab=120/24=5 (A)
U1=U2=Iab*(1/R1+1/R2)^-1=5*6=30 (В)
I1=U1/R1=30/12=2,5 (А)
I2=U2/R2=30/12=2,5 (A)
U3=U4=Iab*(1/R3+1/R4)^-1=5*12=60 (В)
I3=U3/R3=60/20=3 (A)
I4=U4/R4=60/30=2 (A)
U5=I5*R5=5*6=30 (В)
P1=I1*U1=2,5*30=75 (Вт)
P2=I2*U2=2,5*30=75 (Вт)
P3=I3*U3=3*60=180 (Вт)
P4=I4*U4=2*60=120 (Вт)
P5=I5*U5=5*30=150 (Вт)
Pab=Iab*Uab=5*120=600 (Вт)
Дано:
L=150 см;
_________
Найти: t
Задачу можно несколько перефразировать - три куска стержня из одного материала но разной массы, имеющие различные начальные температуры привели в соприкосновение, какая температура установится после наступления теплового равновесия?
Обозначим удельную теплоемкость материала стержня за c. Массы кусков будут пропорциональны их длинам, так как стержень однороден и имеет постоянную площадь поперечного сечения (из графика):
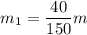
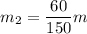
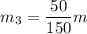
Уравнение теплового баланса будет иметь вид (учтем, что Q>0 если кусок нагревается и Q<0 если остывает):
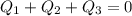
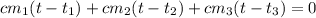

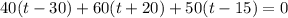
Найдем установившуюся температуру стержня t:
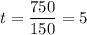 °C
°C
ответ: 5 °С.
Дано:
L=150 см;
_________
Найти: t
Задачу можно несколько перефразировать - три куска стержня из одного материала но разной массы, имеющие различные начальные температуры привели в соприкосновение, какая температура установится после наступления теплового равновесия?
Обозначим удельную теплоемкость материала стержня за c. Массы кусков будут пропорциональны их длинам, так как стержень однороден и имеет постоянную площадь поперечного сечения (из графика):
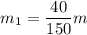
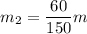
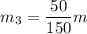
Уравнение теплового баланса будет иметь вид (учтем, что Q>0 если кусок нагревается и Q<0 если остывает):
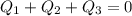
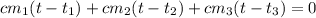

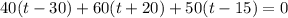
Найдем установившуюся температуру стержня t:
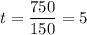 °C
°C
ответ: 5 °С.
Исходная схема представляет собой смешанный (параллельно-последовательный) тип соединения резисторов.
Схему можно преобразовать. Резисторы R₁ и R₂ так же, как и R₃ и R₄ являются парами параллельно соединенных резисторов. (см. рис.)
Поэтому, считая эти пары за отдельные резисторы R₁₂ и R₃₄, можно представить схему в виде трех последовательно соединенных резисторов: R₁₂; R₃₄ и R₅.
Сопротивление R₁₂ = R₁R₂/(R₁+R₂) = 144 : 24 = 6 (Ом)
Сопротивление R₃₄ = R₃R₄/(R₃+R₄) = 600 : 50 = 12 (Ом)
Общее сопротивление цепи:
Rab = R₁₂ + R₃₄ + R₅ = 6 + 12 + 6 = 24 (Ом)
Полный ток в цепи:
I = U/R = 120 : 24 = 5 (A)
Напряжение на резисторах R₁ и R₂:
U₁ = U₂ = I · R₁₂ = 5 · 6 = 30 (B)
Напряжение на резисторах R₃ и R₄:
U₃ = U₄ = I · R₃₄ = 5 · 12 = 60 (B)
Напряжение на резисторе R₅:
U₅ = I · R₅ = 5 · 6 = 30 (B)
Ток, протекающий через R₁:
I₁ = I₂ = U₁₂/R₁ = 30 : 12 = 2,5 (A)
Ток, протекающий через R₃:
I₃ = U₃/R₃ = 60 : 20 = 3 (A)
Ток, протекающий через R₄:
I₄ = U₄/R₄ = 60 : 30 = 2 (A)
Ток, протекающий через R₅
I₅ = U₅/R₅ = 30 : 6 = 5 (A)
Мощность всей цепи:
Рab = U · I = 120 · 5 = 600 (Вт)
Мощность на резисторе R₁ и R₂:
Р₁ = Р₂ = U₁ · I₁ = 30 · 2,5 = 75 (Вт)
Мощность на резисторе R₃:
Р₃ = U₃ · I₃ = 60 · 3 = 180 (Вт)
Мощность на резисторе R₄:
Р₄ = U₄ · I₄ = 60 · 2 = 120 (Вт)
Мощность на резисторе R₅:
Р₅ = U₅ · I₅ = 30 · 5 = 150 (Вт)