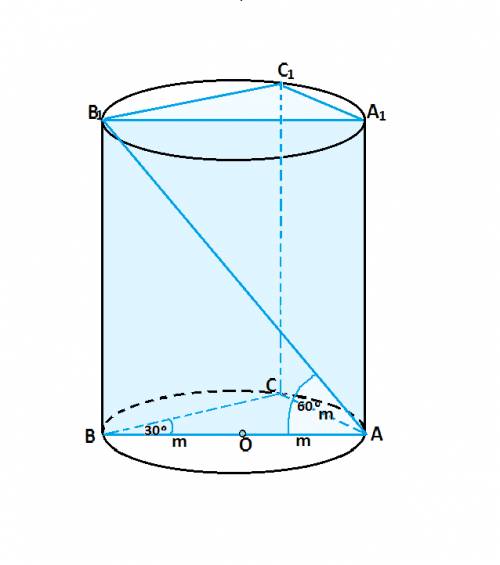
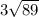
Объяснение:
Объём пирамиды:
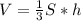, где S - площадь основания, h - высота пирамиды.
Значит 
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна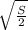 
Тогда, по теореме Пифагора:
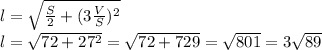
1:7
Объяснение:
Отметим точку L - точку пересечения BC и прямой, проходящей через K параллельно AC.
∠LKM=∠CAM как соответственные углы при параллельных AC и KL и секущей AK.
Поэтому треугольники AMC и KML подобны (в них также есть общий угол AMC).
Отсюда CL:CM=AK:AM=AK:(AK+KM)=1:4.
LB = 2 * CM - CL, поэтому
CL:LB=1:(4 * 2 - 1)=1:7