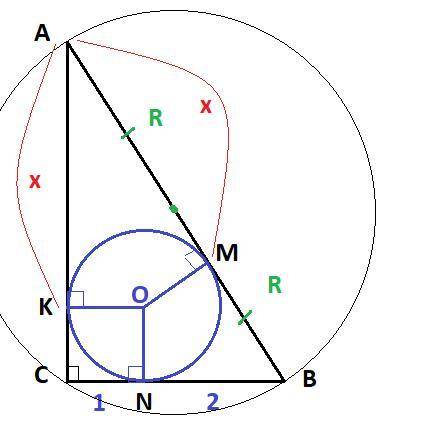
Дано : ΔABC, ∠C = 90°, CN = 1 см, NB = 2 см,
вписанная окружность (O; r)
Найти : S, r, R
Так как окружность вписана в треугольник, то стороны треугольника являются касательными к окружности. Радиус, проведённый в точку касания, перпендикулярен касательной в этой точке.
ON⊥CB, OK⊥AC, OM⊥AB
⇒ CKON - квадрат со стороной, равной радиусу вписанной окружности
⇒ r = CK = KO = JN = CN = 1 см
Отрезки касательных к окружности, проведённые из одной точки, равны
BM = BN = 2 см; AK = AM = x см
ΔABC :
BC = CN + BN = 1 см + 2 см = 3 см
AC = AK + KC = (x + 1) см
AB = AM + MB = (x + 2) см
Площадь прямоугольного треугольника можно вычислить через полупроизведение катетов или через произведение полупериметра на радиус вписанной окружности.
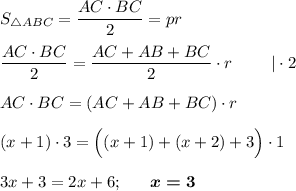
AC = x + 1 = 4 см; AB = x + 2 = 5 см
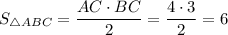 см²
см²
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы
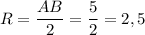 см
см
ответ : S = 6 см², r = 1 см, R = 2,5 см
Дан ромб ABCD; AB=5см; AC+BD=18см.
Найти S(ABCD).
Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть AC∩BD=O.
AO+BO = AC:2+BD:2 = (AC+BD):2 = 18см:2 = 14см
ΔABO - прямоугольный (∠O=90°). Пусть AO=x см, тогда BO=14-х см
По теореме Пифагора:
AO²+BO² = AB² ⇒ x²+(14-x)²=100²
2x²-28x+96 = 0; x²-14x+48 = 0; x(x-8)-6(x-8) = 0; (x-8)(x-6) = 0
x=6 или x=8
Если AO=6см, то ВО=8см, АС=12см, BD=16см
Если АО=8см, то ВО=6см, АС=16см, BD=12см
Получается ABCD это ромб с диагоналями, равными 16см и 12см.
Площадь ромба равна полупроизведению его диагоналей.
S(ABCD) = = 16·12:2 см² = 8·12 см² = 96см²
ответ: 96см².
Объяснение: