уравнения прямой на плоскости
1) для прямой m1 m2 написать уравнение с угловым коэффициентом, в отрезках и общее уравнения. начертить график прямой.
м1 (1: 0)
м2 (-2: -4)
2) в треугольнике m0 m1 m2 найти уравнение медианы, высоты, проведённых из верины m0, а также уравнение средней линии ef, параллельной основанию m1 m2. вычислить длинну найденной высоты
m0 (2; -3)
m1 (1; 0)
m2 (-2; -4)
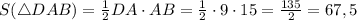 кв. см
кв. см кв. см
кв. см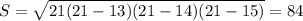 кв.см
кв.см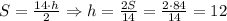 см
см

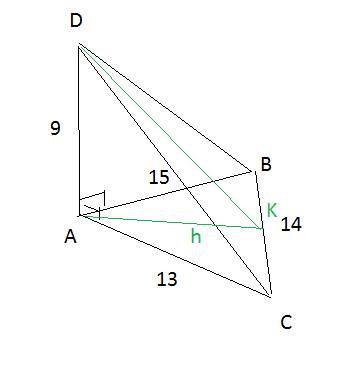
Данная фигура - это трапеция. Площадь трапеции равна произведению полусуммы её оснований на высоту:
S=(9 см + 4 см)/2 × 4 см=26 см²
Чтобы вычислить периметр необходимо найти длины боковых сторон. Найдём их, используя теорему Пифагора (квадрат гипотенузы равен сумме квадратов катетов). В первом треугольнике катеты равны 4 см.
(4² + 4²) см² = 32 см²
√(32 см²)=4√2 см
Во втором треугольнике один катет равен 4 см, а другой - 1 см.
(4² + 1²) см²=17 см²
√(17 см²)=√17 см
Отсюда периметр равен:
9 см + 4 см + 4√2 см + √17 см = 13 см + 4√2 см + √17 см (≈22,8 см)
ответ: S=26 см²; P=13 см + 4√2 см + √17 см