Площадь трапеции S=156 см²
Объяснение:
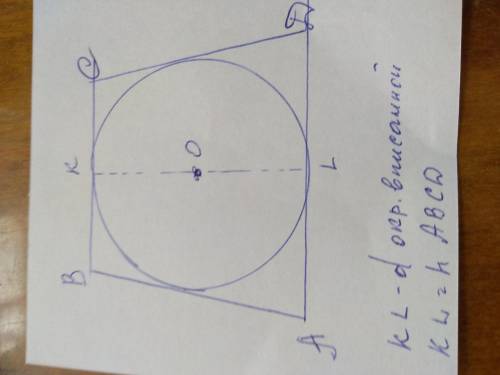
Окружность можно вписать в трапецию тогда и только тогда, когда сумма ее боковых сторон, равна сумме оснований т,е AB+CD= AD+BC
13+13=26см ( AD+BC ), отсюда - сумма оснований AB+CD=26см,
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
S=(а+b):2*h
Высота равнобокой трапеции АВСD равна диаметру вписаной окружности. Зная длинну вписанной окружности в трапецию АВСD, найдем ее диаметр по формуле: P=πd , где P-длинна окружности, которая по условию задачи равна 12πсм.
Подставляем известные значения в формулу и находим диаметр:
12π= πd
d =12π:π; d=12см
Площадь трапеции S=26:2*12=156 см²
6см, 7см.
Объяснение:
Стороны подобных треугольников пропорциональны. Найдём коэффициент подобия, он равен отношению длин меньших сторон подобных треугольников. У первого треугольника меньшей является сторона с длиной 20 см, у второго - 5 см, тогда
k = 20/5 = 4.
Получили, что длины сторон первого трегольника в 4 раза больше соответствующих длин сторон второго треугольника, тогда
24 : 4 = 6 (см) - длина средней стороны второго треугольника,
28 : 4 = 7 (см) - длина большей стороны второго треугольника.
ответ: 6см, 7см.