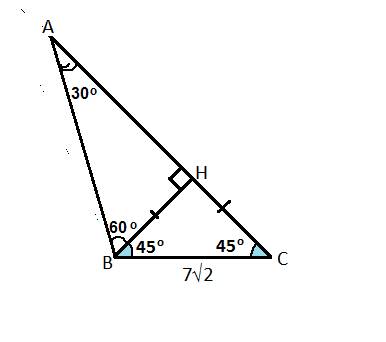
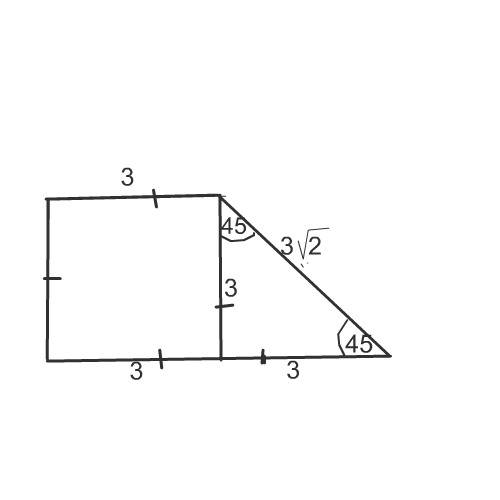
Сделаем рисунок к задаче.
Высота этой трапеции отсекает от нее прямоугольный равнобедренный треугольник с гипотенузой 3√2.
Такой треугольник - половина квадрата с диагональю=гипотенузе.
Формула диагонали квадрата ( формула гипотенузы равнобедренного прямоугольного тр-ка).
d=а√2, где а- сторона квадрата, а в равнобедренном прямоугольном треугольнике - катет. Знание этой формулы часто избавляет от лишних вычислений.
d=СК
СК =3√2=СН√2
СН√2=3√2
СН=3 см
СН=НК как равный катет.
АК=2НК
ВС=АК:2
Площадь трапеции равна Н*(АВ+ВС)
S=3*(3+6):2=13,5 см²
ответ: 420 см² .
Объяснение:
АВСД - трапеция, АД||ВС , АД>ВС , АВ=СД=25 см , АД=36 см , АС=29 см.
Рассмотрим ΔАСД. Найдём его площадь по формуле Герона.
р=1/2*(29+25+36)=45
S=√(45*16*20*9)=9*5*4*2=360
C другой стороны S(АCД)=1/2*36*h=360 , 18*h=360 ⇒ h=CH=360:18=20
h=CH⊥АД
Рассм. ΔСНД: НД=√(СД²-СН²)=√(25²-20²)=√225=15
h=CH⊥АД , АН=АД-НД=36-15=21
ВК⊥АД , АК=НД , ВС=АН-АК=21-15=6
S(АВСД)=(36+6)/2*20=420) (см²)