Итак. Давайте построим нашу трапецию с диагональю, при этом достроив высоты АЕ и DF.
FC = BC - BF
FC = (b - a)/2
Из треугольника FDC по т.Пифагора выразим DF:
DF² = DC² - FC²
DF² = c² - ((b - a)/2)²
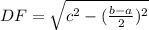
BF = b - (b - a)/2 = (2b - b +a)/2 = (b + a) /2
BD² = DF² + BF²
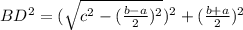
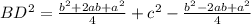
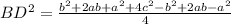
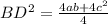
BD² = ab + c²
А BD - и есть диагональ нашей трапеции. А значит:
d² = ab + c²
ЧТД
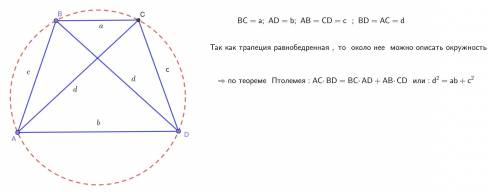
A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
Решение : ///////////////////////////