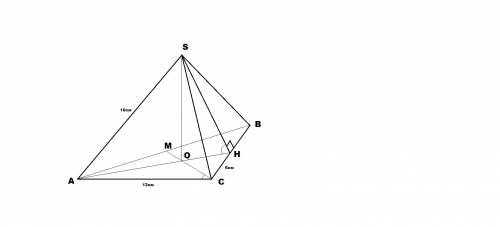
ABCS-прав пирамида АВ=ВС=СА=12см AS=BS=CS=10cm
1) высоту пирамиды
проведем СМ и АН- высоту( медиану, биссектрису) О- ортоцентр АВС
АО=СО=2ОН- по св-ву медиан
рассмотрим тр-к НАС-прямоугольный АС=12смСН=6см, из тПифагора найдем АН=sqrt(AC^2-CH^2) AH=6sqrt3 ( 6 корней из3)=> СО=АО=4sqrt3cm
рассмотрим тр-к SOC-прямоугольный СО=4sqrt3cm SC=10cm из тПифагора найдем SO=sqrt ( SC^2- OC^2) SO=sqrt (100-48)= 2sqrt13cm
2. Угол, образованный боковым ребром и плоскостью основания пирамиды
из треугольника SOC-прямоугольного cosC= OC /SC = 4sqrt3 /10 =2/5sqrt3 C~46*
3. Угол между боковой гранью и плоскостью основания пирамиды
проведем SH- апофему, угSHO- линейный угол двугранного АСВS (CB)
рассмотрим SHO-прямоугольный SOH=90* SO=2sqrt13cm OH=2sqrt3 (по св-ву медиан)
tgH=SO/OH= 2sqrt13 / 2sqrt 3=sqrt (13/3) угН~60*
4. Площадь боковой поверхности
Sбок= 3 S (SBC)
S (BSC)=1/2 BC*SH SH=sqrt(10^2-6^2)=4sqrt3cm
S(BSC)=1/2*12*4sqrt3=24sqrt3cm^2
Sбок= 3 * 24sqrt3=72sqrt3
1. Медиана = высота образует 2 равнобедренных прямоугольных треугольника. 2 стороны при основании равны и = 4 => основание исходного треугольника = 8 см. А стороны при основании =
2. Аналогично первому случаю имеем основание 6 см, а стороны при основании
3. диагональ прямоугольника образует 2 прямоугольных треугольника и является их гипотенузой. Катеты - стороны. По теореме Пифагора получаем
4. Трапеция равнобокая. Высота отсечет от нее прямоугольный треугольник с гипотенузой - боковой стороной = 5см и вторым катетом = (14-8)/2=3 см. Тогда высота трапеции =