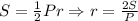
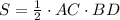
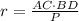
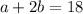Найдите перриметр треугольника абс .аб на 3.6 больше ас.этот треугольник прямоугольный и дан еще внешний угол который равен 120 градусов.этот угол находится возле угла с получается он с ним смежный.ас=5 показано
решить

👇

Ответ:

Ayei

12.04.2022

Рассмотрим треугольник АВС с прямым углом А. Внешний угол при вершине угла С=120 гр. Катет АС=5см, Найдём АВ=5+3,6=8,6 см. Угол АСВ смежен с внешним углом равным 120 гр. Значит угол АСВ=180-120=60 гр. Угол В= 90-60=30гр (сумма острых углов прямоугольного треугольника равна 90 гр).

Катет лежащий против угла 30 гр равен половине гипотенузы. Значит гипотенуза ВС=2АС=2*5=10 см.

Р=10+8,6+5=23,6 см

Если не сойдётся с рисунком напиши, а я перерешаю.

4,5(44 оценок)

Открыть все ответы

Ответ:

oljkejik

12.04.2022

Площадь треугольника равна половине произведение его периметра на радиус вписанной окружности:
$S= \frac{1}{2} Pr\Rightarrow r= \frac{2S}{P}$

С другой стороны площадь можно найти как половина произведения основания на высоту:
$S= \frac{1}{2} \cdot AC\cdot BD$
Тогда выражение для радиуса вписанной окружности примет вид:
$r= \frac{AC\cdot BD}{P}$

Основание АС нам неизвестно, поэтому введем обозначения: AC=a, AB=BC=b, и составим систему уравнений:
Первое уравнение: a+2b=18

- периметр треугольника.
В качестве второго уравнения рассмотрим теорему Пифагора для прямоугольного треугольника BCD, где DC=а/2, так как BD - высота равнобедренного треугольника, а следовательно, и медиана.
Второе уравнение: $( \frac{a}{2} )^2+3^2=b^2$
$\begin{cases} a+2b=18 \\ ( \frac{a}{2} )^2+3^2=b^2\right \end{cases}
\\\
\begin{cases} a=18-2b \\ ( \frac{18-2b}{2} )^2+9=b^2\right \end{cases}
\\\
( 9-b)^2+9=b^2
\\\
81-18b+b^2+9=b^2
\\\
18b=90
\\\
b=5
\\
a=18-2\cdot5=8
\\\
\Rightarrow AC=8$

Подставляем числовые данные в выражения для радиуса:
$r= \frac{AC\cdot BD}{P}= \frac{8\cdot3}{18} = \frac{4}{3}$

ответ: 4/3

Дано: δabc, ab=bc, bd⊥ac, pδ=18, bd=3 найти: r (радиус вписанной окружности) решение:

Дано: δabc, ab=bc, bd⊥ac, pδ=18, bd=3 найти: r (радиус вписанной окружности) решение:

4,5(53 оценок)

Ответ:

Dufrenb

12.04.2022

рассмотрим прямоугольный треугольник ABC в которм угол А - прямой, угол В = 30 градусам а угол С = 60.

Приложим к треугольнику АВС равный ему треугольник АВD. Получим треугольник BCD в котором B = D = 60 градусов, следовательно DC = BC. Но по построению АС 1/2 ВС, ч т д

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30 градусам.

рассмотрим прямоугольный треугольник АВC, у которого катет АС равен половине гипотенузы АС.

Приложим к треугольнику АВС равный ему треугольник ABD. Получит равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу, поэтому каждый из них = 60 градусам. Но угол DBC = 2 угла ABC, следовательно угол АВС = 30 градусов,ч т д

4,4(62 оценок)

Это интересно:

Компьютеры-и-электроника

29.01.2021

Как легко изменить свой идентификатор Apple ID...

Мир-работы

19.10.2021

Как отменить собеседование на работу и не потерять репутацию...

Здоровье

09.08.2022

Как избавиться от круглых щек: эффективные советы для вас...

Транспорт