S∆JAB=12см²
Sпр=120см²
Объяснение:
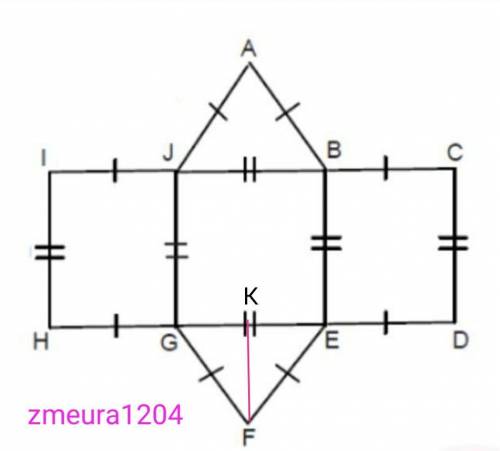
Данная фигура треугольная призма в основании равнобедренный треугольник.
GF=FE=5см, по условию.
ЕВ=ВJ=JG=GE=6см по условию это квадрат.
Проведём в треугольнике ∆GFE, высоту FK.
FK-высота и медиана, так как треугольник равнобедренный.
КЕ=GE:2=6:2=3см.
∆КFE- прямоугольный треугольник.
По теореме Пифагора
КF=√(FE²-KE²)=√(5²-3²)=√(25-9)=4 см
S∆FGE=1/2*KF*GE=1/2*4*6=12 см².
S(GJBE)=BE²=6²=36см²
S(BCDE)=BC*CD=5*6=30 см²
S∆FGE=S∆JAB.
S(BCDE)=S(IJGH)
Sпр=2*S∆FGE+2*S(BCDE)+S(GJBE)=
=2*12+36+2*30=24+36+60=120см² площадь полной поверхности призмы.
Возьмите любой листок бумаги. В центре листа поставьте точку. Это будет первая вершина A создаваемого треугольника.
2Раскройте циркуль на расстояние, точно соответствующее требуемой стороне создаваемого треугольника. Жестко зафиксируйте ножки циркуля в данном положении.
3Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.
4В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.
5Аналогичным поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.
6В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.
7Получив все три вершины, соедините их прямыми линиями с любой ровной поверхности (лучше линейки). Треугольник ABC построен.