Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Объяснение:
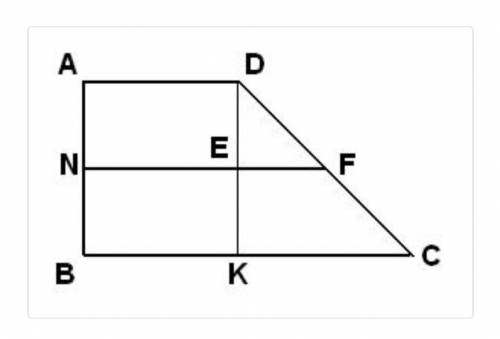
DK – перпендикуляр к ВС (см.рисунок). Так как NF - средняя линия трапеции, то AN = NB = DE = EK = AB/2 = 12/2 = 6 cм. Поскольку угол BCD = 45 градусов, то и угол NFD = 45. Тогда DE = EF = 6 см. Следовательно NE = BK = AD = NF – EF = 20 – 6 = 14 cм. В треугольнике DKC EF – его средняя линия. Посему KC = 2EF = 2*6 = 12 см. Таким образом ВС = ВК + КС. Но выше было найдено, что ВК = NE = AD = 14 см. Тогда ВС = 14 + 12 = 26 см. ВС можно было бы найти и иначе. Помните? Средняя линия трапеции равна полусумме оснований. Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Ну, первая проще некуда - умножаем 4*6 - это площадь одной боковой стороны, и еще умножаем на 4(стороны) Итого 4*6*4=96см^2
2. по апофеме и высоте вычисляем половину длины стороны основания пирамиды. Это по формуле (10^2-8^2) и все это под корнем. получается 6, еще умножаем на 2=12 (сторона основания)
далее вычисляем площадь по формуле: S=(1/2)PL+Sосн, где Р-периметр основания (12*4=48), L-апофема, Sосн-площадь основания (12*12=144). Итого (1/2)*48*10+144=384см^2
3 не знаю до конца, можно вычислить верхние и нижние диагонали по той же формуле, что и в пред. задаче, получается 8корней из 2 и 18корней из 2 соответственно. Если найдешь высоту усеченной пирамиды, можно будет узнать площадь сечения.
Рассмотрим ΔACM:
∠AMC = 180 - ∠CML = 180 - 96= 84 - т. к. смежные углы
Пусть ∠LAC = ∠LCA = x
тогда
1.5x = 96 (180 - 84 = 96 по теореме о сумме углов Δ)
x = 52
значит ∠ALC = 180 - 2*96 = 12
Объяснение: