1) AB = 15
2) AB = 20
Объяснение:
Первый случай, кода AB не пересекает плоскость.
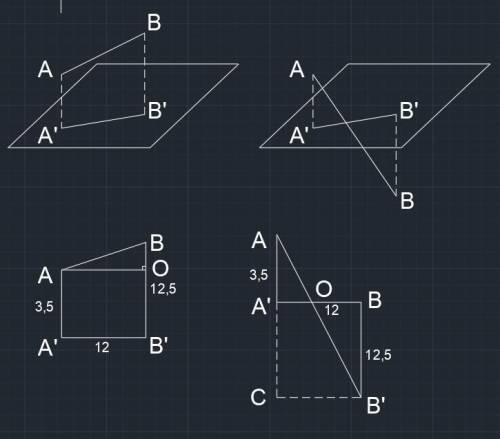
Тогда получаем прямоугольную nрапецию ABB'A'. О - точка пересечения высоты, опущенной из точки A на сторону BB'.
Получаем прямоугольный треугольник ABO
OB=BB'-AA' = 12.5-3.5 = 9
AO = A'B' = 12
По теореме Пифагора получаем
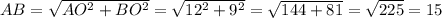
Второй случай, когда AB пересекает плоскость.
Тогда получаем фигуру из двух подобных треугольников (подобие по двум углам, один прямой, второй накрест лежащий, но этот факт нам не понадобится).
Достроим прямоугольный треугольник с прямым углом С продлив сторону AA' восстановив перпендикуляр к этой стороне из точки B.
Получаем прямоугольный треугольник ABC, при этом
AC = AA' + BB' = 12.5+3.5=16
BC = A'B = 12
По теореме Пифагора получаем
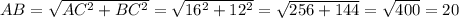
Написала на картинке.
1. Каждая сторона треугольника меньше суммы двух других сторон. Пользуясь этой теоремой, пишем неравенства для сторон шестиугольника.
2. Неравенство для второго вопроса -
PK+KL+LM+MN+NR+PR < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR.
3. Неравенство для третьего вопроса -
2*(PK+KL+LM+MN+NR+PR) < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR+(PK+KL+LM+MN+NR+PR).
4. На картинке.
5. Пользуемся ответами от 3 и 4 задания.Сумма периметров треугольников АВС и DEF равна 16 см (7 см+9 см). Я не знаю, там нужно писать единицы измерения или нет.
Вот такое неравенство в итоге получилось -
2*(PK+KL+LM+MN+NR+PR) < 16 см.
6. Логично, что поделить на 2.
Получаем, что -
2*(PK+KL+LM+MN+NR+PR) < 16 см
PK+KL+LM+MN+NR+PR < 8 см.
Это нам и нужно было доказать!



или 6см и 6 см
или 9 см и 4 см
S = а*в
6*6 = 36 см²
9*4 = 36 см²
Объяснение: