Высота делит прямой угол на 2+1=3 части. каждая по 90°:3=30°.
Меньшая часть= 30°, большая =60°
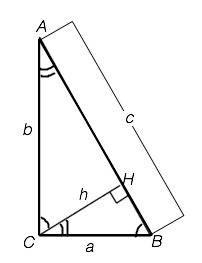
Высота прямоугольного треугольника к гипотенузе делит его на треугольники, подобные друг другу и исходному.
⇒ в ∆ АВС угол А=30° (см.рисунок).
Примем меньший катет равным а, он противолежит углу 30°, поэтому гипотенуза равна 2а ( свойство).
Второй катет АС=2а•cos30°=a√3
Площадь прямоугольного треугольника равна половине произведения катетов.
S=a•b:2
2S=a•а√3
4√3=a²√3⇒
a²=4,⇒ a=2
S (АВС)=AB•h:2
h=2S:2a=4√3:4=√3
Возьмем стороны за 2x, 3x, 4x. В этом случае отношение сохраняется.
Тогда:
abc=24
2x * 3x * 4x = 24
24x³ = 24
x³=1
x=1
Следовательно стороны равны 2, 3, 4 см. Площадь параллелепипида S = 2(ab + ac + bc)
S = 2(6 + 8 + 12)
S = 52 см²
ответ: S = 52 см²