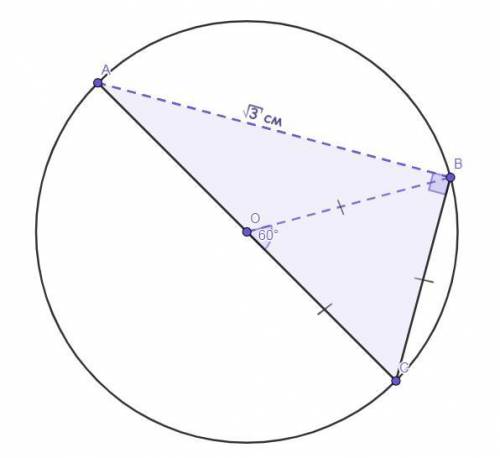
На круге размещены токчи А, В и С так, что АС - диаметр круга, а хорду ВС видно с центра окружности круга под углом в 60°. Найдите радиус круга, если АВ = 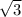 см.
см.
- - -
Дано :Круг.
Точка О - центр данного круга.
Точка А ∈кругу.
Точка В ∈кругу.
Точка С ∈кругу.
АС - диаметр круга.
∠ВОС = 60°.
АВ = 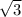 см.
см.
ОС = ? (или ОА, это неважно, так как они равны).
Решение :∠АВС - вписанный (по определению), так ещё и опирается на диаметр АС, следовательно, ∠АВС = 90° (так как диаметр "стягивает" дугу в 180°).
Рассмотрим ΔАВС - прямоугольный.
ОС = ОА (так как радиусы одной окружности). Тогда отрезок ОВ - медиана (по определению), причём проведённая к гипотенузе (АС - гипотенуза, так как лежит против угла в 90°).
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.Следовательно -
ОВ = ВС = ОС.
Тогда ΔОВС - равносторонний (по определению).
Каждый угол равностороннего треугольника равен 60°.Следовательно -
∠ВОС = ∠ОВС = ∠С = 60°.
Тогда -
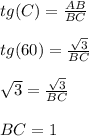
BC = 1 см.
ответ :1 см.
а) Доказательство:
По теореме о сумме углов в треугольнике:
∠С = 180° - ∠A - ∠B = 180° - 40° - 100° = 40°.
Если ∠С = 40°, то ∠С = ∠A. Из этого следует, что △ABC - равнобедренный (BA = BC), что и требовалось доказать.
б) Решение:
Выше мы уже доказали, что △ABC - равнобедренный (BA = BC).
В равнобедренном треугольнике высота, проведённая из вершины угла, противоположного основанию (в данном случае из ∠B), является также его биссектрисой.
Биссектриса делит угол пополам. Отсюда ∠ABH = ∠CBH. А если ∠B = 100°, то ∠ABH = ∠CBH = 100° / 2 = 50°.
ответ: 50°.
a + (5/3)*a + c = 45;
По теореме косинусов (учитываем cos(120) = -1/2; тут 120 градусов конечно)
a^2 +(5*a/3)^2 + 2*a*(5*a/3)*(1/2) = c^2;
a^2*(1 + 25/9 + 5/3) = c^2;
a^2*(49/9) = c^2; c = 7*a/3;
Поэтому
a*(8/3 + 7/3) = 45; a = 9; c = 21;