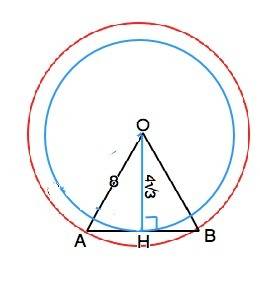
Окружность, вписанная в правильный многоугольник, и окружность, описанная около него, имеют общий центр, причем, так как стороны многоугольника - касательные для вписанной окружности, её радиус является высотой равнобедренного треугольника соединяющего центр с вершинами описанного многоугольника. (см. рисунок).
На рисунке О - центр окружностей, ОА=ОВ=R=8, ОН=r=4√3. Треугольник ОНВ прямоугольный. Sin∠OAH=ОН:ОА=4√3:8=√3/2 - это синус 60°. Следовательно, в равнобедренном треугольнике углы при АВ=60°, ⇒ ∠АОВ=60°, а ∆ АОВ - равносторонний. Сторона данного многоугольника АВ=8. Угол АОВ - центральный, делит окружность на 360°:60°=6 равных углов, противолежащих каждой стороне многоугольника. ⇒ Данный многоугольник имеет 6 сторон.
В данной задаче может быть два случая:
Как мы знаем, в равнобедренном треугольнике боковые стороны равны.
Значит, у нас есть два случая, если боковая сторона равняется 6 или 8.
1) Если боковые стороны равны по 6 см. Значит, основание равно 8 см. Периметр равнобедренного треугольника равен произведение двух боковых сторон плюс основание треугольника. Найдем периметр треугольника в первом случае:
6 · 2 + 8 = 20 см.
2) Если боковые стороны равны по 8 см. Значит, основание равно 6 см.
Найдем периметр:
8 · 2 + 6 = 22 см.
ответ: Первый случай периметр равен 20 см; Второй случай периметр равен 22 см.