
Дано: 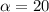 градусов - вписанный угол
градусов - вписанный угол 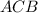
Пусть 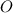 - центр данной окружности
- центр данной окружности
Тогда 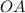 - радиус данной окружности и тогда по свойству касательной
- радиус данной окружности и тогда по свойству касательной
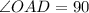 градусов-------(*)
градусов-------(*)
Рассмотрим треугольник 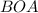 . Этот треугольник равнобедренный (
. Этот треугольник равнобедренный (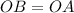 как радиусы). Поэтому по признаку равнобедренного треугольника имеем:
как радиусы). Поэтому по признаку равнобедренного треугольника имеем:
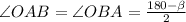 ------(1)
------(1)
где 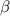 - градусная мера центрального угла
- градусная мера центрального угла 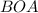
Из свойства вписанного угла имеем:
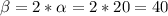 градусов--------(2)
градусов--------(2)
Подставим в (1) вместо 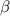 его значение:
его значение:
угол 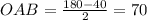 градусов-------(3)
градусов-------(3)
По основному свойству измерения углов найдем искомый угол:
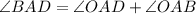 --------(4)
--------(4)
C учетом равенств (*) и (3) равенство (4) примет вид:
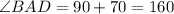 градусов
градусов
Объяснение:
∆ABC = ∆A1B1C1, тo ∠A = ∠A1 ⇒ ∆ABD = ∆A1B1D1 по ги потенузе и острому углу ⇒ BD = B1D1