Пусть h₁ - высота параллелограмма, a - его основание, b - основание равнобедренного треугольника, h₂ - высота равнобедренного треугольника, c - его боковая сторона. Площадь параллелограмма равна произведению основания на высоту: В равнобедренном треугольника высота, проведённая к основанию, является медианой и биссектрисой. По теореме Пифагора (рассматривается треугольник, образованный высотой, а не весь равнобедренный треугольник): Тогда Площадь треугольника равна половине произведения основания на высоту: Т.к. площади треугольника и параллелограмма равны, то ответ: 2.
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть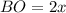 см и
см и 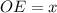 см, тогда
см, тогда 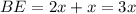 , что по условию он равен 9 см.
, что по условию он равен 9 см.
Следовательно,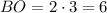 см и
см и 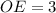 см
см
Аналогично, пусть теперь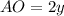 см и
см и 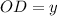 , тогда
, тогда 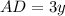 и по условию равен 12 см
и по условию равен 12 см
Таким образом,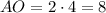 см и
см и 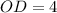 см.
см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника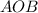
По теореме Пифагора из прямоугольного треугольника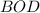
Тогда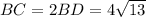 см
см
Из прямоугольного треугольника по теореме Пифагора
по теореме Пифагора
Тогда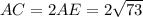 см
см
ответ: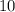 см;
см; 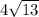 см;
см; 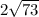 см.
см.