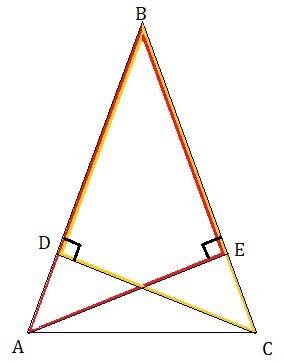
∠BEA = ∠BDC = 90° (так как AE и CD — высоты △ABC).
⟹ треугольники ABE и CBD прямоугольные.
Сумма острых углов прямоугольного треугольника равна 90°.
В треугольнике ABE ∠BAE = 90° — ∠B.
В треугольнике CBD ∠BCD = 90° — ∠B.
⟹ ∠BAE = ∠BCD, ∠B — общий,
BA = BC (как боковые стороны равнобедренного △ABC)
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
⟹ треугольники ABE и CBD равны.
Из равенства треугольников следует равенство соответствующих сторон: AE = CD.
Что и требовалось доказать.
1. Расстояние от центра окружности до точки, из которой проведены две касательные, делит угол A пополам. Значит угол HAO равен 30 градусам. Проведем радиус от точки O в точку касания окружности с касательной. Радиус, проведенный из центра окружности к точке касания является перпендикуляром к касательной. Получается прямоугольный треугольник HAO. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов половине гипотенузы. OA - гипотенуза
OH=1/2*6
OH=3
OH-радиус окружности
ответ:R=3
2.28 градусов
3.7