Я опробовала много решения задачи — зная радиус, но в конце концов сделала вывод, что он нам совсем не нужен.
Нам достаточно знать всего лишь отрезки, полученные делением точки касания на гипотенузе.
Теорема о касательных такова: 2 касательные, проведённые с одной точки, в точках касания — равны друг другу.
То есть: BE == BD = 12 (так как оба отрезка проведены с общей точки B).
И ещё: FC == DC = 18 (то же определение).
И также: KE == KF (оба проведены с одной точки (K)).
По теореме Пифагора, гипотенуза равна: 
Найдём Дискриминант:
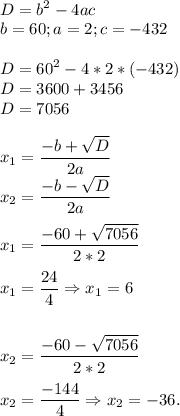
Следовательно:
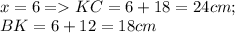
Следовательно:
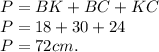
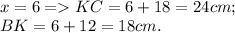
Вывод: KC = 24см; BK = 18см; P = 72см.
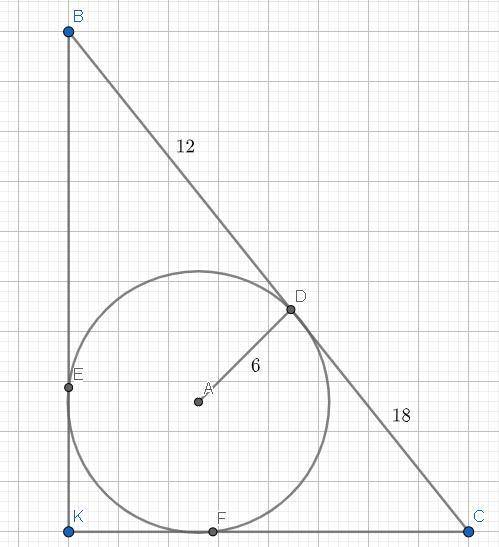
Рассмотрим ∆ АВD и ∆ СВЕ
Оба прямоугольные и имеют общий острые угол АВС.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Из подобия следует отношение
ВЕ:ВD=ВС:АВ⇒ВD•ВС=ВЕ•АВ ⇒
ВЕ:ВС=ВD:АВ
Две стороны ∆ ВЕD пропорциональны двум сторонам треугольника АВС, и угол между ними общий.
2-й признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Следовательно, ∆АВС и ∆ ВЕD подобны, что и требовалось доказать.
Можно добавить. что коэффициент подобия равен косинусу общего угла, т.к. отношение катетов ∆ СВЕ и ∆ АВД к их гипотенузам соответственно равны косинусу угла В треугольника АВС.