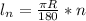В треугольнике ABC даны LA = 90°, В= 60°, AC = 9. Найдите
сторону AB.

Решение.

По условию задачи ZA = — , следовательно, отрезок АС –
катет, противолежащий углу , и требуется найти катет, при-
лежащий к углу.

Отношение катета, противолежащего углу B, и катета, прилежа-
щего к этому углу, есть

угла В, следователь-
но,
—. Отсюда AB = AC :

- : tg 60°=
ответ.

👇

Увидеть ответ

Ответ:

Элиза12098

07.11.2021

В треугольнике ABC даны ∠A = 90°, В= 60°, AC = 9. Найдите

сторону AB.

Решение.

По условию задачи ∠A = 90° , следовательно, отрезок АС –

катет, противолежащий ∠В , и требуется найти катет, при-

лежащий к ∠В.

Отношение катета, противолежащего ∠ B, и катета, прилежа-

щего к этому углу, есть тангенс угла В, следовательно, АС/АВ=tgB.

Отсюда AB = AC : tgB=9 : tg 60°= 9/√3=3√3

ответ: АВ=3√3

4,7(72 оценок)

Открыть все ответы

Ответ:

Амиiskdhdm

07.11.2021

1. $l_{n} = \frac{\pi R}{180} *n$ , где n - градусная мера соответственного центрального угла.
Найдем радиус окружности:
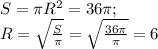$S= \pi R^{2} =36 \pi ; \\ 
R= \sqrt{ \frac{S}{ \pi } } = \sqrt{ \frac{36 \pi }{ \pi } }=6$ , где S - площадь круга.
Найдем длину дуги:
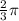$l_{20}= \frac{6 \pi }{180} *20= \frac{2}{3} \pi$
ответ: $\frac{2}{3} \pi$ см.
2. Найдем сторону квадрата a:
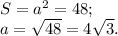
$S= a^{2} = 48; \\ 
a= \sqrt{48} =4 \sqrt{3}.$
Радиус вписанной в квадрат окружности равен:
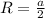$R= \frac{a}{2}$ , где a - сторона квадрата.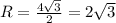
$R= \frac{4 \sqrt{3} }{2} =2 \sqrt{3}$
Площадь вписанного треугольника равна:
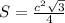$S= \frac{ c^{2} \sqrt{3} }{4}$ , где c - сторона правильного треугольника.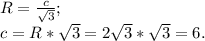
Необходимо найти сторону правильного треугольника. Так как нам известен радиус описанной около треугольника окружности, то воспользуемся формулой:
$R= \frac{c}{ \sqrt{3} } ; \\ 
c=R* \sqrt{3} =2 \sqrt{3} * \sqrt{3} =6.$
Найдем площадь правильного треугольника:
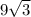$S= \frac{ c^{2} \sqrt{3} }{4} = \frac{36 \sqrt{3} }{4} =9 \sqrt{3}$ .
ответ: $9 \sqrt{3}$ см.

4,4(56 оценок)

Ответ:

lisa22151

07.11.2021

1) Диагонали параллелограмма равны. НЕВЕРНО

Диагонали равны только у разновидностей параллелограмма : у прямоугольника и квадрата.

2) Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы. ВЕРНО

3) В прямоугольной трапеции ровно один прямой угол. НЕВЕРНО

Боковая сторона, которая образует прямой угол с одним основанием трапеции, является перпендикуляром к двум параллельным основаниям, значит, она образует прямой угол со вторым основанием тоже. Всего в прямоугольной трапеции 2 прямых угла. Если в трапеции будет 4 прямых угла, то это будет прямоугольник.

4) Сумма углов четырёхугольника равна 360°. ВЕРНО

4,6(38 оценок)

Это интересно:

Финансы-и-бизнес

01.02.2020

Как купить марки, не выходя из дома: советы и рекомендации...

Искусство-и-развлечения

07.01.2021

Как скрыться: лучшие способы оставаться невидимым...

Компьютеры-и-электроника

25.08.2022

Как удалить iSearch AVG - подробная инструкция...