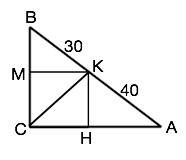
Все углы четырехугольника МКНС, вписанного в прямоугольный треугольник АВС – прямые, две стороны равны по условию, две другие им параллельны и противолежат, поэтому он – квадрат.
Его диагональ СМ для прямого угла С является биссектрисой.
Биссектриса угла треугольника делит противолежащую этому угла сторону на отрезки, пропорциональные прилежащим сторонам. ⇒
ВС:АС=ВК:АК.
Обозначим АС=х, ВС=у. ⇒
у:х=30:40 ⇒ у:х=3:4 ⇒
у=3х/4
АВ=30+40=7•10
По т.Пифагора
АВ²=АС²+ВС²=х²+у² Заменим у на его значение, выраженное через х:
7²•10²=х²+ 9х²/16
7²•10²=25x²/16
25x²=49•100•16
x²=49•4•16 ⇒x=7•2•4=56 см – длина АС
ВС=3•56/4=42 см
Выведу обобщённую формулу для подобных задач про трапецию с известными диагоналями AC = x, BD = y, и суммой оснований BC + AD = m
Проведём из вершинны С прямую СЕ, параллельную BD, тогда BC || DE, CE || BD ⇒ BCED - параллелограми, ВС = DE, CE = BD = y
S (abcd) = (BC + AD)•CH/2 = (DE + AD)•CH/2 = AE•CH/2 = S (ace)
Площадь трапеции ABCD равна площади треугольника ACE
Найдём плошадь ΔАСЕ по формуле Герона: АС = х, CE = y, AE = m
Площадь трапеции с диагоналями х и у и суммой оснований равной m:S = √( p • (p - x) • (p - y) • (p - m) ) , где р = (х + y + m)/2Средняя линия трапеции: MN = (BC + AD)/2 = 5 ⇒ m = 10, x = 9, у = 17
S (abcd) = √(18•(18 - 9)(18 - 17)(18 - 10)) = √(18•9•1•8) = 36ответ: 36