30°
Объяснение:
В равнобедренном треугольнике два угла одинаковые (у основания), а третий отличается. Сумма углов треугольника = 180°.
Т.о. может быть два варианта:
1. Углы у основания больше в 2,5 раза третьего угла
2. Углы у основания меньше в 2,5 раза третьего угла
Пусть углы у основания будут = a = b
Третий угол c
Вариант 1:
a = b = 2.5 c
a + b + c = 180°
2,5c + 2,5c + c = 180°
6c = 180°
c = 180°/3 = 30°
Наименьший угол с = 30°
Вариант 2:
a = b = c/2.5 = c*(2/5)
a + b + c = 180°
c * (2/5) + c* (2/5) + c = 180°
c ( 1 + 4/5) = 180°
c = 5* 180°/9 = 100°
a = b = c*2/5 = 40°
В первом вартанте наимельший уголо меньше. Значит ответ задачи 30°
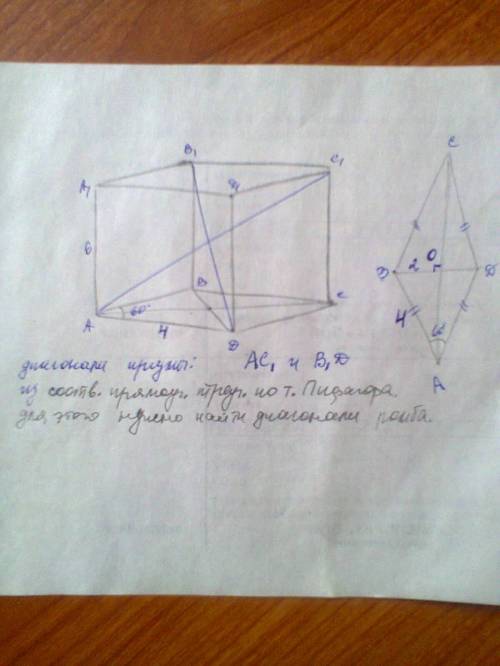
Диагонали ромба точкой пересечения делятся пополам (как и у параллелограмма)
Диагонали ромба взаимно перпендикулярны
Диагонали ромба являются биссектрисами его углов
из треуг.BOA: угол BAO=30, катет BO = 4/2 = 2 (катет против угла в 30 град.=половине гипотенузы) и по т.Пифагора второй катет = корень(4^2-2^2) = 2корень(3)
следовательно, диагонали ромба равны
BD = 2BO = 4
AC = 2AO = 4корень(3)
AC1^2 = AC^2 + CC1^2 = 4*4*3 + 6*6 = 4*(12+9) = 4*21
AC1 = 2корень(21)
B1D^2 = BD^2 + CC1^2 = 4+36 = 40
B1D = 2корень(10)
1. Соединим точки С и D с центром. Тогда треугольники AOD и ВОС равнобедренные (OA = OB = OC = OD как радиусы), ⇒
∠1 = ∠2 и ∠3 = ∠4.
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АВ. Но тогда в этих треугольниках равны и углы при вершине О. Значит треугольники AOD и ВОС равны по двум сторонам и углу между ними, ⇒
AD = BC.
2. Точки, находящиеся на данном расстоянии от данной прямой а, будут расположены на прямой, параллельной прямой а (красные прямые). В зависимости от расположения прямых задача может иметь одно решение (1), два решения (2) и не иметь решения (3).
Поскольку углы при основе равны, то облзначим их через Х, а верхний угол - 2.5Х. Тогда:
4.5Х = 180;
Х = 180/4.5 = 40.
ответ: 40