Объяснение:
Дано:
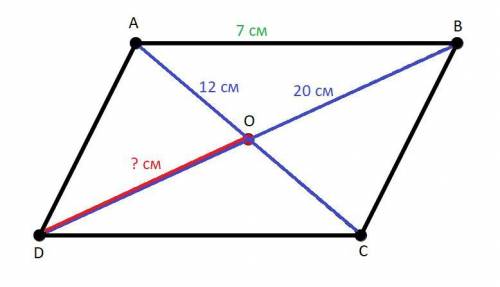
ABCD - параллелограмм.
AC и BD - диагонали параллелограмма.
AC ∩ BD = O.
AC = 12 (см); BD = 20 (см); AB = 7 (см).
Найти:
DO - ? (см).
Тут всё довольно просто. Так как ABCD - параллелограмм, вспомним свойство такой геометрической фигуры: диагонали параллелограмма точкой пересечения делятся пополам. Т.е. диагонали AC и BD делятся точкой пересечения O пополам. Соответственно DO будет равняться половине всей диагонали BD. (и из этого следует, что DO = OB)
DO = BD/2 = 20 : 2 = 10 (см)
L(дуги) = α*R ( α - центральный угол в радианах )
α = 60 ° = π /3 рад
L(дуги) = (π /3)*R =(π /3)*12 см = 4π.
* (60° /360°) =1/6 часть длины окружности: L(дуги) =(1/6)*2πR =πR/3 *
----------------------
C =2πR =π*2R =π*b/sin∠B= π*b/sin(180°-(30°+30°) =
π*b/sin(180°- 60°) =π*b/sin60°= π*10/(√3 /2 ) =(20/√3)π =
(20√3 / 3)π.