Элементарно, Ватсон! ;)
Как известно, ромб обладает следующим замечательными свойствами, которые мы применим при решении данной задачи:
"Площадь ромба равна половине произведения его диагоналей"
"Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам"
Отсюда следует что площадь ромба равна:
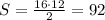см²
Длина стороны ромба равна:
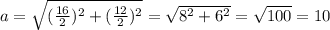см
Поскольку площадь одной боковой грани равна:
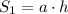находим высоту призмы 
:
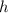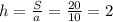см
Объём призмы, таким образом равен:
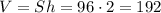см²
Как "Лучшее решение" отметить не забудь, ОК?!.. ;)))
точно незнаю как вы решаете но у меня есть 2 варианта
1)Диагональ куба
Следовательно, ребро куба a=6/корень из 3 = 2*корень из трёх
Диагональ куба, его ребро и диагональ основания образуют равносторонний треугольник, в котором углы при основании равны 45 градусам: (180-90):2 = 45
Косинус 45 градусов = 0,7071
2)
1)Квадрат диагональ грани d²=a²+a². Квадрат диагональ куба D²=a²+a²+a². По условиюD=√(3a²)=a√3=6 => a=2√3.
Косинус угла гранью и диагональю куба равен косинусу угла между диагональю грани и диагональю куба
cosφ=a√2/(a√3)=√2/√3
а)ДС параллельно СД
ДД1 -высота на пл. α =а/2
СС1 -высота на пл. α =ДД1=а/2
б)линейный угол двугранного угла DABM -это угол между плоскостями которым принадлежат прямые ДА и ВМ
в)
ДД2 -высота на АВ
ДД2=ДА*sin60=a√3/2
sinДД2Д1=ДД1/ДД2=(а/2)/(a√3/2)=1/√3.