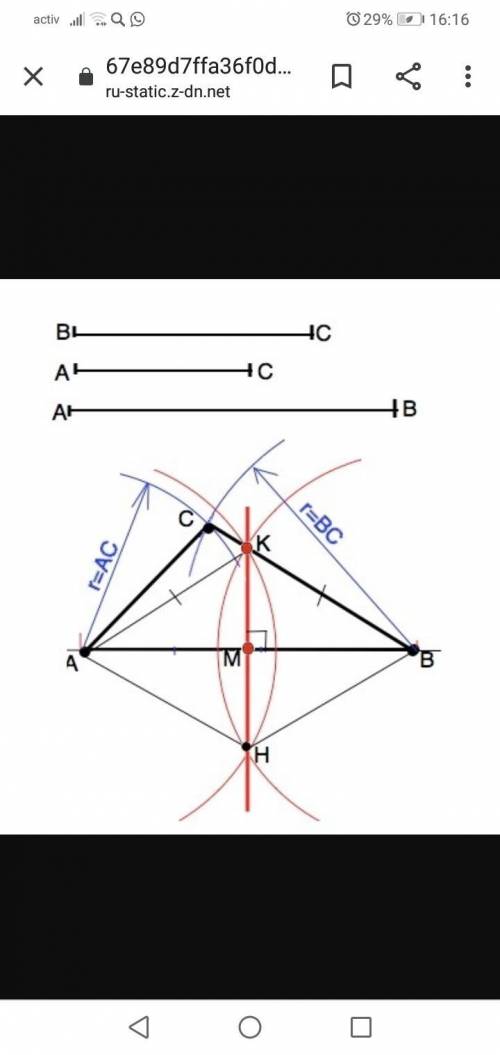
ответ:. На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг - вершина С искомого треугольника.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса, но больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
Точно так же делят отрезок пополам.
Объяснение: делал на скорую руку
Длина высоты будет равна 4,8 единиц
Это решается очень просто.
Прямоугольные треугольники обладают таким свойством, что высота, опущенная на гипотенузу из прямого угла, делит треугольник на 2 ему подобных.
Из подобия одного треугольника к исходному и теоремы Пифагора - вытекает решение.
Синусы и косинусыТолько задачка, скорее всего, из такого класса, что синусы еще не проходили. Поэтому подобие - наиболее приемлемое должно быть. иначе учитель запалит решение.
Можно из подобия треугольников, можно изходить из косинуса/синуса одного из углов, но получается пропорция:
h/a=b/c, где a,b -катеты, с-гипотенуза, h-высота
h=ab/c=6*8/SQRT(6^2+8^2)=48/10=4.8